Directed acyclic graph
A directed acyclic graph (DAG) is a directed graph that contains no cycles. DAGs arise in a natural way in modelling situations in which, in some sense, going "forward" is sometimes possible but going "backward" is definitely not, so that if  is reachable from
is reachable from  , we know that
, we know that  is not reachable from
is not reachable from  (unless
(unless  ). An example is given by Water Park from CCC 2007. In the absence of mechanical intervention, water always flows from high altitudes to low altitudes, so that, when travelling along the waterslides, one can never arrive at the same spot twice. If we create a graph that has a vertex for each marked point in the water park and a directed edge from
). An example is given by Water Park from CCC 2007. In the absence of mechanical intervention, water always flows from high altitudes to low altitudes, so that, when travelling along the waterslides, one can never arrive at the same spot twice. If we create a graph that has a vertex for each marked point in the water park and a directed edge from  to
to  whenever there is a water slide from
whenever there is a water slide from  to
to  , this graph will be acyclic, and hence a DAG. DAGs do not necessarily resemble undirected acyclic graphs (that is, forests) in form or in their properties; there may be multiple paths between a given pair of nodes.
, this graph will be acyclic, and hence a DAG. DAGs do not necessarily resemble undirected acyclic graphs (that is, forests) in form or in their properties; there may be multiple paths between a given pair of nodes.
As a partial order
DAGs are often considered representations of partial orderings. We can establish a correspondence as follows:
- Give each vertex of the DAG a unique label (such as the letters A, B, C, etc.). Each label corresponds to an element in our set.
- We define our partial ordering as follows:
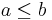 in the ordering if and only if there exists a path from
in the ordering if and only if there exists a path from  to
to  , where
, where  is the vertex in the DAG labelled with
is the vertex in the DAG labelled with 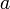 and
and  is the vertex in the DAG labelled with
is the vertex in the DAG labelled with 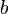 .
.
The ordering thus defined is reflexive, since every vertex is reachable from itself. It is antisymmetric, because if 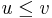 and
and 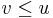 , and
, and 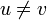 , then we have a cycle that contains
, then we have a cycle that contains 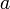 and
and 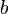 , a contradiction. And it is transitive because reachability is transitive; if there are paths from
, a contradiction. And it is transitive because reachability is transitive; if there are paths from  to
to  and from
and from  to
to 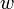 then we can concatenate them to obtain a path from
then we can concatenate them to obtain a path from  to
to 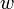 . So the ordering we have defined is a partial ordering.
. So the ordering we have defined is a partial ordering.
Note that whereas a given DAG will correspond to exactly one partial ordering (up to isomorphism) using this convention, there may be more than one DAG that corresponds to a given partial ordering. The DAG with the greatest number of edges that corresponds to a given partial ordering is known as the transitive closure, whereas the one with the fewest number of edges is known as the transitive reduction.