Difference between revisions of "Directed acyclic graph"
(Created page with "A '''directed acyclic graph (DAG)''' is a directed graph that contains no cycles. DAGs arise in a natural way in modelling situations in which, in some sense, going "forward"...") |
(→Problems: - longest path) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 7: | Line 7: | ||
The ordering thus defined is reflexive, since every vertex is reachable from itself. It is antisymmetric, because if <math>u \leq v</math> and <math>v \leq u</math>, and <math>u \neq v</math>, then we have a cycle that contains <math>a</math> and <math>b</math>, a contradiction. And it is transitive because reachability is transitive; if there are paths from <math>u</math> to <math>v</math> and from <math>v</math> to <math>w</math> then we can concatenate them to obtain a path from <math>u</math> to <math>w</math>. So the ordering we have defined is a partial ordering. | The ordering thus defined is reflexive, since every vertex is reachable from itself. It is antisymmetric, because if <math>u \leq v</math> and <math>v \leq u</math>, and <math>u \neq v</math>, then we have a cycle that contains <math>a</math> and <math>b</math>, a contradiction. And it is transitive because reachability is transitive; if there are paths from <math>u</math> to <math>v</math> and from <math>v</math> to <math>w</math> then we can concatenate them to obtain a path from <math>u</math> to <math>w</math>. So the ordering we have defined is a partial ordering. | ||
| − | Note that whereas a given DAG will correspond to exactly one partial ordering (up to isomorphism) using this convention, there may be more than one DAG that corresponds to a given partial ordering. The DAG with the | + | Note that whereas a given DAG will correspond to exactly one partial ordering (up to isomorphism) using this convention, there may be more than one DAG that corresponds to a given partial ordering. The DAG with the most edges that corresponds to a given partial ordering is known as the [[transitive closure]], whereas the one with the fewest edges is known as the [[transitive reduction]]. |
| + | |||
| + | ==Properties== | ||
| + | A '''source''' is a node with zero in-degree; all edges point outward. Likewise, a '''sink''' is a node with zero out-degree. Every finite DAG has at least one source and one sink. To see this, choose any node. If it is a sink we are done; otherwise select any outgoing edge and follow it to another node. Repeating this process, we will never repeat a node, because the graph has no cycles, so after <math>V-1</math> iterations (where <math>V</math> is the number of nodes in the graph), this process must terminate. The proof that there must be at least one source is analogous. | ||
| + | |||
| + | In fact, a stronger statement holds: a directed graph may be ''[[Topological sort|topologically ordered]]'' if and only if it is acyclic (a DAG). | ||
| + | |||
| + | Because a DAG has no cycles, each vertex in a DAG forms a separate strongly connected component. | ||
| + | |||
| + | A DAG with <math>V</math> vertices cannot have more than <math>V(V-1)/2</math> edges, and this bound is attained by taking a complete undirected graph on <math>V</math> vertices, assigning a different number to each vertex, and orienting all edges so that they point from the lower-numbered vertex to the higher-numbered vertex. Such a DAG represents a total order. The proof is not hard and is left as an exercise to the reader. | ||
| + | |||
| + | ==Problems== | ||
| + | The following problems either involve DAGs specifically or have simpler/faster solutions for DAGs than for other graphs. | ||
| + | * The '''[[topological sort]]ing''' problem mentioned in the preceding section. | ||
| + | * '''[[Shortest paths]]''' and '''transitive closure''' | ||
| + | :* '''Single-source shortest paths''' can be computed in <math>O(E+V)</math> time by topologically sorting first and then using [[dynamic programming]]. | ||
| + | :* '''[[All-pairs shortest paths]]''' can be computed in <math>O(V(E+V))</math> by <math>V</math> invocations of the single-source algorithm. This is, however, no faster than [[breadth-first search]] when the DAG is unweighted, and no faster than the [[Floyd–Warshall algorithm]] when the graph is dense (so that it is an improvement only over sparse weighted DAGs). | ||
| + | ::* The same applies to the '''transitive closure problem''' – it is not easy to improve over the <math>O(V^3)</math> bound given by Warshall's algorithm, but see [[Directed acyclic graph/Transitive closure|this]] for a method that may perform better under certain circumstances. The bounds on the '''transitive reduction problem''' match those on transitive closure. | ||
| + | * '''Longest path problem''': This can also be solved efficiently using dynamic programming. Note that we only need to consider paths that start at a source. | ||
| + | * Identifying all strongly connected components in a digraph and contracting each component to a single vertex produces a DAG, known as the '''kernel DAG'''. Adapting the special transitive closure algorithm on DAGs to the kernel DAG gives an algorithm which may be fast for some classes of digraphs. The kernel DAG is also useful as an intermediate structure in the solutions of various other problems. | ||
| + | * The '''[[minimum spanning arborescence]] problem''' does not have much to do with DAGs in general, but an arborescence is a specific kind of DAG that looks like a tree. | ||
Latest revision as of 05:36, 18 March 2011
A directed acyclic graph (DAG) is a directed graph that contains no cycles. DAGs arise in a natural way in modelling situations in which, in some sense, going "forward" is sometimes possible but going "backward" is definitely not, so that if  is reachable from
is reachable from  , we know that
, we know that  is not reachable from
is not reachable from  (unless
(unless  ). An example is given by Water Park from CCC 2007. In the absence of mechanical intervention, water always flows from high altitudes to low altitudes, so that, when travelling along the waterslides, one can never arrive at the same spot twice. If we create a graph that has a vertex for each marked point in the water park and a directed edge from
). An example is given by Water Park from CCC 2007. In the absence of mechanical intervention, water always flows from high altitudes to low altitudes, so that, when travelling along the waterslides, one can never arrive at the same spot twice. If we create a graph that has a vertex for each marked point in the water park and a directed edge from  to
to  whenever there is a water slide from
whenever there is a water slide from  to
to  , this graph will be acyclic, and hence a DAG. DAGs do not necessarily resemble undirected acyclic graphs (that is, forests) in form or in their properties; there may be multiple paths between a given pair of nodes.
, this graph will be acyclic, and hence a DAG. DAGs do not necessarily resemble undirected acyclic graphs (that is, forests) in form or in their properties; there may be multiple paths between a given pair of nodes.
As a partial order[edit]
DAGs are often considered representations of partial orderings. We can establish a correspondence as follows:
- Give each vertex of the DAG a unique label (such as the letters A, B, C, etc.). Each label corresponds to an element in our set.
- We define our partial ordering as follows:
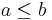 in the ordering if and only if there exists a path from
in the ordering if and only if there exists a path from  to
to  , where
, where  is the vertex in the DAG labelled with
is the vertex in the DAG labelled with  and
and  is the vertex in the DAG labelled with
is the vertex in the DAG labelled with  .
.
The ordering thus defined is reflexive, since every vertex is reachable from itself. It is antisymmetric, because if 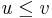 and
and 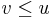 , and
, and 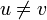 , then we have a cycle that contains
, then we have a cycle that contains  and
and  , a contradiction. And it is transitive because reachability is transitive; if there are paths from
, a contradiction. And it is transitive because reachability is transitive; if there are paths from  to
to  and from
and from  to
to 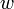 then we can concatenate them to obtain a path from
then we can concatenate them to obtain a path from  to
to 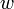 . So the ordering we have defined is a partial ordering.
. So the ordering we have defined is a partial ordering.
Note that whereas a given DAG will correspond to exactly one partial ordering (up to isomorphism) using this convention, there may be more than one DAG that corresponds to a given partial ordering. The DAG with the most edges that corresponds to a given partial ordering is known as the transitive closure, whereas the one with the fewest edges is known as the transitive reduction.
Properties[edit]
A source is a node with zero in-degree; all edges point outward. Likewise, a sink is a node with zero out-degree. Every finite DAG has at least one source and one sink. To see this, choose any node. If it is a sink we are done; otherwise select any outgoing edge and follow it to another node. Repeating this process, we will never repeat a node, because the graph has no cycles, so after 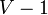 iterations (where
iterations (where  is the number of nodes in the graph), this process must terminate. The proof that there must be at least one source is analogous.
is the number of nodes in the graph), this process must terminate. The proof that there must be at least one source is analogous.
In fact, a stronger statement holds: a directed graph may be topologically ordered if and only if it is acyclic (a DAG).
Because a DAG has no cycles, each vertex in a DAG forms a separate strongly connected component.
A DAG with  vertices cannot have more than
vertices cannot have more than 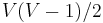 edges, and this bound is attained by taking a complete undirected graph on
edges, and this bound is attained by taking a complete undirected graph on  vertices, assigning a different number to each vertex, and orienting all edges so that they point from the lower-numbered vertex to the higher-numbered vertex. Such a DAG represents a total order. The proof is not hard and is left as an exercise to the reader.
vertices, assigning a different number to each vertex, and orienting all edges so that they point from the lower-numbered vertex to the higher-numbered vertex. Such a DAG represents a total order. The proof is not hard and is left as an exercise to the reader.
Problems[edit]
The following problems either involve DAGs specifically or have simpler/faster solutions for DAGs than for other graphs.
- The topological sorting problem mentioned in the preceding section.
- Shortest paths and transitive closure
- Single-source shortest paths can be computed in
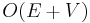 time by topologically sorting first and then using dynamic programming.
time by topologically sorting first and then using dynamic programming. - All-pairs shortest paths can be computed in
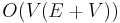 by
by  invocations of the single-source algorithm. This is, however, no faster than breadth-first search when the DAG is unweighted, and no faster than the Floyd–Warshall algorithm when the graph is dense (so that it is an improvement only over sparse weighted DAGs).
invocations of the single-source algorithm. This is, however, no faster than breadth-first search when the DAG is unweighted, and no faster than the Floyd–Warshall algorithm when the graph is dense (so that it is an improvement only over sparse weighted DAGs).
- The same applies to the transitive closure problem – it is not easy to improve over the
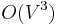 bound given by Warshall's algorithm, but see this for a method that may perform better under certain circumstances. The bounds on the transitive reduction problem match those on transitive closure.
bound given by Warshall's algorithm, but see this for a method that may perform better under certain circumstances. The bounds on the transitive reduction problem match those on transitive closure.
- The same applies to the transitive closure problem – it is not easy to improve over the
- Single-source shortest paths can be computed in
- Longest path problem: This can also be solved efficiently using dynamic programming. Note that we only need to consider paths that start at a source.
- Identifying all strongly connected components in a digraph and contracting each component to a single vertex produces a DAG, known as the kernel DAG. Adapting the special transitive closure algorithm on DAGs to the kernel DAG gives an algorithm which may be fast for some classes of digraphs. The kernel DAG is also useful as an intermediate structure in the solutions of various other problems.
- The minimum spanning arborescence problem does not have much to do with DAGs in general, but an arborescence is a specific kind of DAG that looks like a tree.