Difference between revisions of "Convex hull trick"
| Line 17: | Line 17: | ||
<p>Thus, if we remove "irrelevant" lines such as <math>y=4</math> in this example (the lines which will never give the minimum <math>y</math>-coordinate, regardless of the query value) and sort the remaining lines by slope, we obtain a collection of <math>N</math> intervals (where <math>N</math> is the number of lines remaining), in each of which one of the lines is the minimal one. If we can determine the endpoints of these intervals, it becomes a simple matter to use [[binary search]] to answer each query.</p> | <p>Thus, if we remove "irrelevant" lines such as <math>y=4</math> in this example (the lines which will never give the minimum <math>y</math>-coordinate, regardless of the query value) and sort the remaining lines by slope, we obtain a collection of <math>N</math> intervals (where <math>N</math> is the number of lines remaining), in each of which one of the lines is the minimal one. If we can determine the endpoints of these intervals, it becomes a simple matter to use [[binary search]] to answer each query.</p> | ||
===Etymology=== | ===Etymology=== | ||
| − | The term ''convex hull'' is sometimes misused to mean ''upper/lower envelope''. If we consider the "optimal" segment of each of the three lines (ignoring <math>y=4</math>), what we see is the ''lower envelope'' of the lines: nothing more or less than the set of points obtained by choosing the lowest point for every possible <math>x</math>-coordinate. (The lower envelope is highlighted in green in the diagram above.) Notice that the set bounded above by the lower envelope is convex. We could imagine the lower envelope being the upper convex hull of some set of points, and thus the name ''convex hull trick'' arises. | + | The term ''convex hull'' is sometimes misused to mean ''upper/lower envelope''. If we consider the "optimal" segment of each of the three lines (ignoring <math>y=4</math>), what we see is the ''lower envelope'' of the lines: nothing more or less than the set of points obtained by choosing the lowest point for every possible <math>x</math>-coordinate. (The lower envelope is highlighted in green in the diagram above.) Notice that the set bounded above by the lower envelope is convex. We could imagine the lower envelope being the upper convex hull of some set of points, and thus the name ''convex hull trick'' arises. (Notice that the problem we are trying to solve can again be reformulated as finding the intersection of a given vertical line with the lower envelope.) |
| + | ===Adding a line=== | ||
| + | <p>As we have seen, if the set of relevant lines has already been determined and sorted, it becomes trivial to answer any query in <math>\mathcal{O}(\lg N)</math> time ''via'' binary search. Thus, if we can add lines one at a time to our data structure, recalculating this information quickly with each addition, we have a workable algorithm: start with no lines at all (or one, or two, depending on implementation details) and add lines one by one until all lines have been added and our data structure is complete.</p> | ||
| + | <p>Suppose that we are able to process all of the lines before needing to answer any of the queries. Then, we can sort them in descending order by slope beforehand, and merely add them one by one. When adding a new line, some lines may have to be removed because they are no longer relevant. If we imagine the lines to lie on a [[stack]], in which the most recently added line is at the top, as we add each new line, we consider if the line on the top of the stack is relevant anymore; if it still is, we push our new line and proceed. If it is not, we pop it off and repeat this procedure until either the top line is not worthy of being discarded or there is only one line left (the one on the bottom, which can never be removed).</p> | ||
| + | <p>How, then, can we determine if the line should be popped from the stack? Suppose <math>l_1</math>, <math>l_2</math>, and <math>l_3</math> are the second line from the top, the line at the top, and the line to be added, respectively. Then, <math>l_2</math> becomes irrelevant if and only if the intersection point of <math>l_1</math> and <math>l_3</math> is to the left of the intersection of <math>l_1</math> and <math>l_2</math>. (This makes sense because it means that the interval in which <math>l_3</math> is minimal subsumes that in which <math>l_2</math> was previously.) We have assumed for the sake of simplicity that no three lines are concurrent.</p> | ||
| + | ==Case study: USACO MAR08 acquire== | ||
==References== | ==References== | ||
* Brucker, P. (1995). Efficient algorithms for some path partitioning problems. ''Discrete Applied Mathematics'', 62(1-3), 77-85. | * Brucker, P. (1995). Efficient algorithms for some path partitioning problems. ''Discrete Applied Mathematics'', 62(1-3), 77-85. | ||
Revision as of 05:52, 3 January 2010
The convex hull trick is a technique (perhaps best classified as a data structure) used to determine efficiently, after preprocessing, which member of a set of linear functions in one variable attains an extremal value for a given value of the independent variable. It has little to do with convex hull algorithms.
Contents
History
The convex hull trick is perhaps best known in algorithm competition from being required to obtain full marks in several USACO problems, such as MAR08 "acquire", which began to be featured in national olympiads after its debut in the IOI '02 task Batch Scheduling, which itself credits the technique to a 1995 paper (see references). Very few online sources mention it, and almost none describe it. (The technique might not be considered important enough, or people might want to avoid providing the information to other countries' IOI teams.)
The problem
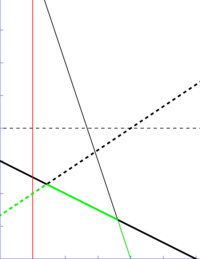
Suppose that a large set of linear functions in the form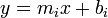 
is given along with a large number of queries. Each query consists of a value of 
and asks for the minimum value of 
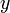that can be obtained if we select one of the linear functions and evaluate it at . For example, suppose our functions are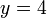 
, 
, 
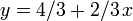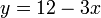, and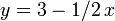 
and we receive the query 
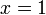. We have to identify which of these functions assumes the lowest 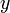-value for 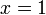, or what that value is. (It is the function 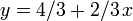, assuming a value of 2.)
-coordinate 1 (shown by the red vertical line), which line is "lowest" (has the lowest 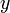-coordinate). Here it is the heavy dashed line, .
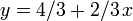Naive algorithm
For each of the 
queries, of course, we may simply evaluate every one of the linear functions, and determine which one has the least value for the given -value. If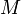 
lines are given along with queries, the complexity of this solution is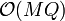 
. The "trick" enables us to speed up the time for this computation to 
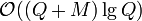, a significant improvement.
The technique
Consider the diagram above. Notice that the line 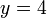will never be the lowest one, regardless of the -value. Of the remaining three lines, each one is the minimum in a single contiguous interval (possibly having plus or minus infinity as one bound). That is, the heavy dotted line is the best line at all -values left of its intersection with the heavy solid line; the heavy solid line is the best line between that intersection and its intersection with the light solid line; and the light solid line is the best line at all -values greater than that. Notice also that, as increases, the slope of the minimal line decreases: 4/3, -1/2, -3. Indeed, it is not difficult to see that this is always true.
Thus, if we remove "irrelevant" lines such as 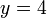in this example (the lines which will never give the minimum 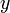-coordinate, regardless of the query value) and sort the remaining lines by slope, we obtain a collection of 
intervals (where is the number of lines remaining), in each of which one of the lines is the minimal one. If we can determine the endpoints of these intervals, it becomes a simple matter to use binary search to answer each query.
Etymology
The term convex hull is sometimes misused to mean upper/lower envelope. If we consider the "optimal" segment of each of the three lines (ignoring 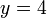), what we see is the lower envelope of the lines: nothing more or less than the set of points obtained by choosing the lowest point for every possible -coordinate. (The lower envelope is highlighted in green in the diagram above.) Notice that the set bounded above by the lower envelope is convex. We could imagine the lower envelope being the upper convex hull of some set of points, and thus the name convex hull trick arises. (Notice that the problem we are trying to solve can again be reformulated as finding the intersection of a given vertical line with the lower envelope.)
Adding a line
As we have seen, if the set of relevant lines has already been determined and sorted, it becomes trivial to answer any query in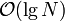 
time via binary search. Thus, if we can add lines one at a time to our data structure, recalculating this information quickly with each addition, we have a workable algorithm: start with no lines at all (or one, or two, depending on implementation details) and add lines one by one until all lines have been added and our data structure is complete.
Suppose that we are able to process all of the lines before needing to answer any of the queries. Then, we can sort them in descending order by slope beforehand, and merely add them one by one. When adding a new line, some lines may have to be removed because they are no longer relevant. If we imagine the lines to lie on a stack, in which the most recently added line is at the top, as we add each new line, we consider if the line on the top of the stack is relevant anymore; if it still is, we push our new line and proceed. If it is not, we pop it off and repeat this procedure until either the top line is not worthy of being discarded or there is only one line left (the one on the bottom, which can never be removed).
How, then, can we determine if the line should be popped from the stack? Suppose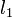 
, 
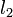, and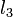 
are the second line from the top, the line at the top, and the line to be added, respectively. Then, 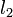becomes irrelevant if and only if the intersection point of 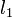and 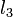is to the left of the intersection of 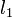and 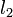. (This makes sense because it means that the interval in which 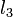is minimal subsumes that in which 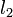was previously.) We have assumed for the sake of simplicity that no three lines are concurrent.
Case study: USACO MAR08 acquire
References
- Brucker, P. (1995). Efficient algorithms for some path partitioning problems. Discrete Applied Mathematics, 62(1-3), 77-85.
