Difference between revisions of "Convex hull trick"
(Created page with 'The '''convex hull trick''' is a technique which is perhaps best known in algorithm competition from being required to obtain full marks in several USACO problems, such as [http:…') |
|||
| Line 1: | Line 1: | ||
| − | The '''convex hull trick''' is a technique which is perhaps best known in algorithm competition from being required to obtain full marks in several USACO problems, such as [http://tjsct.wikidot.com/usaco-mar08-gold MAR08 "acquire"], which began to be featured in national olympiads after its debut in the IOI '02 task [http://ioinformatics.org/locations/ioi02/contest/day2/batch/batch.pdf Batch Scheduling], which itself credits the technique to a 1995 paper (see references). Very few online sources mention it, and almost none describe it. (The technique might not be considered important enough, or people might want to avoid providing the information to other countries' IOI teams.) | + | The '''convex hull trick''' is a technique (perhaps best classified as a data structure) used to determine, after preprocessing, which member of a set of linear functions in one variable attains an extremal value for a given value of the independent variable. It has little to do with [[convex hull]] algorithms. |
| + | |||
| + | ==History== | ||
| + | The convex hull trick is perhaps best known in algorithm competition from being required to obtain full marks in several USACO problems, such as [http://tjsct.wikidot.com/usaco-mar08-gold MAR08 "acquire"], which began to be featured in national olympiads after its debut in the IOI '02 task [http://ioinformatics.org/locations/ioi02/contest/day2/batch/batch.pdf Batch Scheduling], which itself credits the technique to a 1995 paper (see references). Very few online sources mention it, and almost none describe it. (The technique might not be considered important enough, or people might want to avoid providing the information to other countries' IOI teams.) | ||
| + | |||
| + | ==The problem== | ||
| + | <p>Suppose that a large set of linear functions in the form <math>y = m_i x + b_i</math> is given along with a large number of queries. Each query consists of a value of <math>x</math> and asks for the minimum value of <math>y</math> that can be obtained if we select one of the linear functions and evaluate it at <math>x</math>. For example, suppose our functions are <math>y=4</math>, <math>y=\frac{4}{3}+\frac{2}{3}x</math>, <math>y=15-3x</math>, and <math>y=3-\frac{1}{2}x</math> and we receive the query <math>x=1</math>. We have to identify which of htese functions assumes the lowest <math>y</math>-value for <math>x=1</math>, or what that value is. (It is the function <math>y=\frac{4}{3}+\frac{2}{3}x</math>, assuming a value of 2.)</p> | ||
==References== | ==References== | ||
* Brucker, P. (1995). Efficient algorithms for some path partitioning problems. ''Discrete Applied Mathematics'', 62(1-3), 77-85. | * Brucker, P. (1995). Efficient algorithms for some path partitioning problems. ''Discrete Applied Mathematics'', 62(1-3), 77-85. | ||
Revision as of 06:08, 2 January 2010
The convex hull trick is a technique (perhaps best classified as a data structure) used to determine, after preprocessing, which member of a set of linear functions in one variable attains an extremal value for a given value of the independent variable. It has little to do with convex hull algorithms.
History
The convex hull trick is perhaps best known in algorithm competition from being required to obtain full marks in several USACO problems, such as MAR08 "acquire", which began to be featured in national olympiads after its debut in the IOI '02 task Batch Scheduling, which itself credits the technique to a 1995 paper (see references). Very few online sources mention it, and almost none describe it. (The technique might not be considered important enough, or people might want to avoid providing the information to other countries' IOI teams.)
The problem
Suppose that a large set of linear functions in the form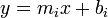 
is given along with a large number of queries. Each query consists of a value of 
and asks for the minimum value of 
that can be obtained if we select one of the linear functions and evaluate it at . For example, suppose our functions are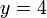 
, 
, 
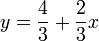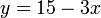, and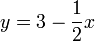 
and we receive the query 
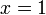. We have to identify which of htese functions assumes the lowest -value for 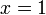, or what that value is. (It is the function 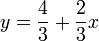, assuming a value of 2.)
References
- Brucker, P. (1995). Efficient algorithms for some path partitioning problems. Discrete Applied Mathematics, 62(1-3), 77-85.
