Convex hull
In computational geometry, the convex hull of a set of points is the smallest convex set (minimal area, volume, etc.) which contains every point in that set.
Contents
Intuitive interpretations for the planar convex hull[edit]
- If a set of points were given in two dimensions by hammering nails into them on a flat wooden board, the convex hull would be the polygon whose boundary is given by stretching and releasing a rubber band around all of the nails.
- If the points represented the locations of sheep grazing in a field, the convex hull would be the minimal-perimeter fence enclosing all of the sheep. [1]
- If the points represented the locations of fence posts, the convex hull would be the fence enclosing the maximum possible area while consisting only of straight segments using those fence posts as endpoints. [2]
- If the points represented the locations of prize-winning maple trees, the perimeter of the convex hull would be the minimum length of blue ribbon required to enclose all of them. [3]
Planar convex hull algorithms[edit]
The problem of finding the convex hull of a set of points in the plane is one of the best-studied in computational geometry and a variety of algorithms exist for solving it. Here are three algorithms introduced in increasing order of conceptual difficulty:
Gift-wrapping algorithm[edit]
The gift-wrapping algorithm, also known as the Jarvis march, is one of the simplest and most intuitive planar convex hull algorithms. The name derives from the analogy of the method to walking around the set of points with gift wrapping paper until arriving back at one's starting location.
The first step in the algorithm is to select a point which must be in the convex hull, for example, the point with highest y-coordinate. The wrapping paper will start here, and we will walk around the point set until we arrive back at this point. Initially we will face the right (increasing x-coordinate). At any given time we maintain both a point  (our location) and a vector
(our location) and a vector  (the direction we are facing). The algorithm then proceeds in a series of steps. In each step, we turn clockwise until we are directly facing a point, say,
(the direction we are facing). The algorithm then proceeds in a series of steps. In each step, we turn clockwise until we are directly facing a point, say, 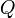 . Then, we walk over to that point (bringing the wrapping paper along with us). In doing so, notice that the new value of
. Then, we walk over to that point (bringing the wrapping paper along with us). In doing so, notice that the new value of  is set to
is set to 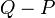 (since that is the direction we now face) and
(since that is the direction we now face) and  is set to
is set to 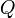 (that's where we are). This procedure is repeated until
(that's where we are). This procedure is repeated until  equals its starting value. After the completion of the algorithm we will have visited all of the points of the convex hull in clockwise order.
equals its starting value. After the completion of the algorithm we will have visited all of the points of the convex hull in clockwise order.
To determine which point we actually see first as we turn clockwise, we loop through all points 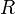 (except for
(except for  itself), for each point considering the vector
itself), for each point considering the vector 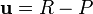 . The
. The 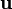 which makes the smallest angle
which makes the smallest angle 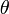 with
with  corresponds to
corresponds to 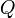 , the point we should visit next. (This makes sense; it means we will have to turn through the smallest possible angle to get there). To minimize
, the point we should visit next. (This makes sense; it means we will have to turn through the smallest possible angle to get there). To minimize 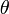 , we maximize
, we maximize 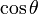 , which can be computed as simply
, which can be computed as simply 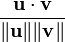 .
.
Each step of the algorithm (picking the next point) requires considering all the other points in the set, so it takes 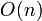 time, where
time, where  is the total number of points. The number of steps executed equals the number of points that are actually on the hull, denoted
is the total number of points. The number of steps executed equals the number of points that are actually on the hull, denoted 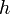 , so the total time taken is
, so the total time taken is 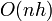 . In the worst case, in which
. In the worst case, in which 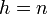 and all the points in the input already form a convex polygon, the performance is
and all the points in the input already form a convex polygon, the performance is 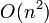 . It is not recommended to use this algorithm when
. It is not recommended to use this algorithm when 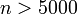 .
.
Graham scan[edit]
The Graham scan has much better worst-case performance than the Jarvis march, but is also more complicated. First, some point (not necessarily one of the points in input) is identified which is definitely inside the convex hull. Averaging the coordinates of all of the points given is the recommended technique for doing so. We place the origin of our coordinate system there, transforming the coordinates of the input points accordingly. We then proceed to sort the points by angle. (That is, for each point  in the input, we consider the directed angle the ray
in the input, we consider the directed angle the ray 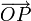 makes with the positive x-axis; we sort in increasing order of this angle.) Ties are broken arbitrarily. Initially we don't know any points which might be in the hull, so we set
makes with the positive x-axis; we sort in increasing order of this angle.) Ties are broken arbitrarily. Initially we don't know any points which might be in the hull, so we set 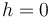 . We then consider all points in order of increasing angle, modifying what we believe to be the hull so far during each step. Denote the current hull
. We then consider all points in order of increasing angle, modifying what we believe to be the hull so far during each step. Denote the current hull 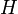 , the point added earliest to
, the point added earliest to 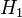 , and so on up to
, and so on up to 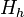 , the point most recently added. In each step we do the following:
, the point most recently added. In each step we do the following:
- Add the current point
 to the end of
to the end of 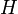 . That is, increment
. That is, increment 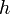 and set
and set 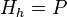 .
. - If
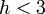 , proceed to the next point.
, proceed to the next point. - Consider the points
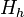 ,
, 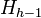 , and
, and 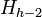 . It is possible that after we have added the point
. It is possible that after we have added the point 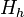 , we are now certain that
, we are now certain that 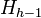 is not actually part of the hull. Consider the vectors
is not actually part of the hull. Consider the vectors 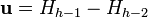 and
and 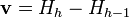 . If
. If  is a counterclockwise turn from
is a counterclockwise turn from 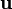 , that is,
, that is, 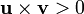 , then everything is fine, and we go on to the next point. But if
, then everything is fine, and we go on to the next point. But if  is a clockwise turn from
is a clockwise turn from 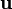 , that is,
, that is, 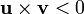 , then the angle
, then the angle 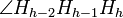 is "concave" and
is "concave" and 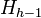 must be removed. This means that
must be removed. This means that 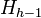 is set to
is set to 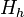 and
and 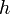 is decremented. Then go back to step 2.
is decremented. Then go back to step 2.
At this point we have a set of points 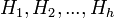 sorted in counterclockwise order. The problem is that we do not actually know whether
sorted in counterclockwise order. The problem is that we do not actually know whether 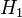 is in the hull or not; notice that it can never be removed during the first phase of the algorithm. Also, since the convex hull is a ring, not a chain, we also have to consider the fact that
is in the hull or not; notice that it can never be removed during the first phase of the algorithm. Also, since the convex hull is a ring, not a chain, we also have to consider the fact that 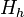 is not really part of the hull either; note that it also wouldn't have been removed during the first phase of the algorithm. The way we eliminated points before was by considering three consecutive points in the hull and deciding whether to remove the middle one. We must now subject
is not really part of the hull either; note that it also wouldn't have been removed during the first phase of the algorithm. The way we eliminated points before was by considering three consecutive points in the hull and deciding whether to remove the middle one. We must now subject 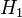 and
and 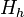 to this repeatedly until no more changes can be made:
to this repeatedly until no more changes can be made:
- Consider the three points
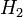 ,
, 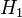 , and
, and 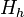 . Let
. Let 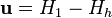 and
and 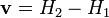 . If
. If 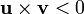 , then
, then 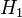 must be removed from the hull.
must be removed from the hull. - Consider the three points
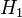 ,
, 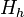 , and
, and 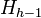 . Let
. Let 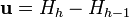 and
and 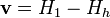 . If
. If 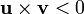 , then
, then 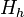 must be removed from the hull.
must be removed from the hull. - If neither of steps 1 and 2 were executed, we are done; what remains is the true convex hull, given in counterclockwise order. Otherwise, go back to step 1.
In order to ensure that we can delete 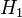 in constant time (which shifts over all the other elements, so that the new
in constant time (which shifts over all the other elements, so that the new 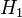 is the old
is the old 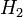 , and so on), we should use a deque or linked list to store
, and so on), we should use a deque or linked list to store 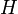 .
.
The initial sort takes 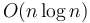 time. In the remainder of the algorithm, each point is added to the hull exactly once, so all the "add" operations take
time. In the remainder of the algorithm, each point is added to the hull exactly once, so all the "add" operations take 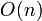 time in total. Each point can also be removed up to once, so all the "remove" operations take
time in total. Each point can also be removed up to once, so all the "remove" operations take 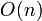 time total. Finally, in each step, in which we may examine several triples of consecutive points to determine if the middle point should be removed, notice that we stop after we encounter a point which should not be removed. That is, in each step, the number of "consider" operations is at most one more than the number of points removed, and hence in total the number of "consider" operations is at most
time total. Finally, in each step, in which we may examine several triples of consecutive points to determine if the middle point should be removed, notice that we stop after we encounter a point which should not be removed. That is, in each step, the number of "consider" operations is at most one more than the number of points removed, and hence in total the number of "consider" operations is at most 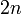 , and take
, and take 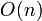 time in total. Overall, the sort dominates the running time, which is
time in total. Overall, the sort dominates the running time, which is 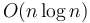 , suitable for almost any application.
, suitable for almost any application.
Monotone chains algorithm[edit]
The monotone chains algorithm is both easy to code (although arguably conceptually difficult) and the fastest of the three algorithms in this section. It is based on computing two "monotone chains" of the convex hull: the upper chain and the lower chain. The leftmost and rightmost points of the input set must both be in the convex hull. The part of the hull clockwise from the leftmost point and counterclockwise from the rightmost point is called the upper chain; the rest is the lower chain. We compute the upper and lower chains separately.
The first step is to sort all of the given points in increasing order of x-coordinate. Ties are broken by increasing order of y-coordinate. We then begin to compute the upper chain. The first point in the set is the leftmost point (or the lowest leftmost point, if there are several), and must be on the hull. We then consider the points in order. Again, denote the current hull as 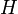 and the size of the hull as
and the size of the hull as 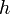 , where
, where 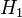 is the first point in the hull and
is the first point in the hull and 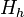 is the last. For each point considered:
is the last. For each point considered:
- Add this point to
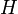 .
. - If
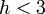 , continue to the next point.
, continue to the next point. - Consider the vectors
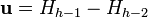 and
and 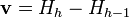 . This time, since we have to travel clockwise to build the upper hull, we check if
. This time, since we have to travel clockwise to build the upper hull, we check if 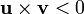 . If so, we proceed to the next point. Otherwise, we remove
. If so, we proceed to the next point. Otherwise, we remove 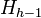 and go back to step 2.
and go back to step 2.
After considering all of the points in this manner, 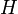 contains the entire upper chain. We then proceed to compute the lower chain in exactly the same way, except that we consider the points in reverse order (that is, we start at the rightmost point). (Take care not to add the rightmost point to the hull twice.) On termination of the algorithm,
contains the entire upper chain. We then proceed to compute the lower chain in exactly the same way, except that we consider the points in reverse order (that is, we start at the rightmost point). (Take care not to add the rightmost point to the hull twice.) On termination of the algorithm, 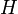 will contain the entire hull in clockwise order, with the first point repeated at the end.
will contain the entire hull in clockwise order, with the first point repeated at the end.
Again, the running time is 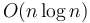 ; the sorting cost dominates. The monotone chains algorithm is the algorithm recommended for all applications, being simpler than the Graham scan and a bit faster (since we don't have to compute angles).
; the sorting cost dominates. The monotone chains algorithm is the algorithm recommended for all applications, being simpler than the Graham scan and a bit faster (since we don't have to compute angles).
Degenerate input[edit]
Ideally, we would like to have the input points in general position, with no two points coincident nor three points lying on the same line. However, this is not always possible, and coincident and collinear points must be dealt with. To lapse into a full discussion of cases would be tedious and boring. Instead, consider the following:
- Read the problem statement for clarification on what to do with degenerate input. (Note that it will almost surely not refer to it as degenerate.)
- If there are coincident points:
- the Jarvis march might divide by zero. This must be avoided to ensure the correctness of the implementation.
- If we only need to report the perimeter or area of the hull, the other two algorithms have no trouble with handling coincident points (except for the pathological case discussed further below for the Graham scan).
- If we actually have to report the points, there are three conceivable orders in which we might be asked to do so: clockwise, counterclockwise, or in the same order as in the input file (increasing "ID"). Clearly the first two are meaningless if coincident points are allowed. In the third, we might be asked to report only the first point if several points are coincident, or to report all of them. Read the problem statement carefully. In any case, we can efficiently postprocess the points to make the output conform to specification. This is probably easier than attempting to compute the correct output exactly while running the convex hull algorithm.
- If there are collinear points:
- We need to know whether the problem statement requires us to output the maximum possible number of points or the minimum possible number of points. That is, should we include points that fall in the interior of an edge in the hull? If there are collinear points but no coincident ones, the Graham scan and the monotone chains algorithm can be used to handle either case gracefully, by using either a
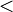 or a
or a 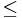 sign in our test. In the Jarvis march, we choose either the closest or the farthest point when there are ties in angle.
sign in our test. In the Jarvis march, we choose either the closest or the farthest point when there are ties in angle. - Ordering is not an issue, unless we're asked to output the maximum possible number of points in increasing order of ID to break ties along edges. In this case, postprocessing is almost certainly the easiest solution.
- We need to know whether the problem statement requires us to output the maximum possible number of points or the minimum possible number of points. That is, should we include points that fall in the interior of an edge in the hull? If there are collinear points but no coincident ones, the Graham scan and the monotone chains algorithm can be used to handle either case gracefully, by using either a
- The worst pathological cases occur when the area of the hull is zero. There are two ways in which this might happen, but both are trivial to handle: all points might be coincident, or all points might lie on a single line. If such cases are allowed to be given in the input:
- The monotone chains algorithm will still work properly if only the perimeter or area needs to be reported.
- If the points themselves need to be reported, it is probably not worth the effort to make the algorithms handle them gracefully; instead, it is trivial to simply compute the hulls separately by sorting the points.
Applications[edit]
Other than the obvious interpretations:
- Farthest pair of points
- Consider the following problem [can someone track down the source, please?]: you are given several colors of paint. Each one was created by mixing together a certain nonzero amount of each of the three primary subtractive colors (cyan, magenta, and yellow), and is hence given as a triplet in the input. Assume that the color of a given mixture depends only on the ratios of the amounts of the three primary colors present. By mixing paints, can we obtain a target color (also given as a triplet)? The amount is not important. It turns out that this problem may be solved using the two-dimensional convex hull. First of all, we normalize each paint by dividing each component by the amount of cyan paint present. (This does not actually change the color, as ratios are preserved.) We do the same for the target triplet. Then we discard all the cyan components entirely, since they are all 1, and focus on the other two components. Each color may then be plotted as a point on the plane. The possible target colors are those which lie inside the convex hull of the colors given. This is because when we mix together two paints, each component of the new color is the same linear combination of the components of the two original paints; since ratios are unimportant we can always normalize the result, so that the cyan 1s will always stay as 1s; and the new point obtained will therefore lie on the line segment joining the two original points. The convex hull is the set of all points reachable by executing this procedure an arbitrary number of times.
Three-dimensional convex hull[edit]
Computing a convex hull in 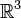 is significantly more challenging. It is a task which will most likely never be given on competitions such as the IOI, and it is not recommended that high school students learn it. However, there is a fairly simple
is significantly more challenging. It is a task which will most likely never be given on competitions such as the IOI, and it is not recommended that high school students learn it. However, there is a fairly simple 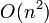 algorithm, which works as follows: first project all of the points onto the xy-plane, and find an edge that is definitely on the hull by selecting the point with highest y-coordinate and then doing one iteration of gift wrapping to determine the other endpoint of the edge. This is the first part of the incomplete hull. We then build the hull iteratively. Consider this first edge; now find another point in order to form the first triangular face of the hull. We do this by picking the point such that all the other points lie to the right of this triangle, when viewed appropriately (just as in the gift-wrapping algorithm, in which we picked an edge such that all other points lay to the right of that edge). Now there are three edges in the hull; to continue, we pick one of them arbitrarily, and again scan through all the points to find another point to build a new triangle with this edge, and repeat this until there are no edges left. (When we create a new triangular face, we add two edges to the pool; however, we have to first check if they have already been added to the hull, in which case we ignore them.) There are
algorithm, which works as follows: first project all of the points onto the xy-plane, and find an edge that is definitely on the hull by selecting the point with highest y-coordinate and then doing one iteration of gift wrapping to determine the other endpoint of the edge. This is the first part of the incomplete hull. We then build the hull iteratively. Consider this first edge; now find another point in order to form the first triangular face of the hull. We do this by picking the point such that all the other points lie to the right of this triangle, when viewed appropriately (just as in the gift-wrapping algorithm, in which we picked an edge such that all other points lay to the right of that edge). Now there are three edges in the hull; to continue, we pick one of them arbitrarily, and again scan through all the points to find another point to build a new triangle with this edge, and repeat this until there are no edges left. (When we create a new triangular face, we add two edges to the pool; however, we have to first check if they have already been added to the hull, in which case we ignore them.) There are 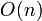 faces, and each iteration takes
faces, and each iteration takes 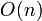 time since we must scan all of the remaining points, giving
time since we must scan all of the remaining points, giving 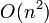 . (If you feel like coding this, you might try CH3D@SPOJ.) It is possible to speed up this algorithm significantly by initially discarding a large number of points we know not to be in the hull; one easy way that performs quite well is to find both extremal points with respect to each of the three coordinate axes, and discard all points in the interior of the octahedron they form.
. (If you feel like coding this, you might try CH3D@SPOJ.) It is possible to speed up this algorithm significantly by initially discarding a large number of points we know not to be in the hull; one easy way that performs quite well is to find both extremal points with respect to each of the three coordinate axes, and discard all points in the interior of the octahedron they form.
It is possible to compute a 3D convex hull in 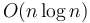 time using a divide-and-conquer algorithm, but this is extremely difficult.
time using a divide-and-conquer algorithm, but this is extremely difficult.