Difference between revisions of "Big numbers"

From PEGWiki
Jump to: navigation, search
Line 4: Line 4:
  
 
==Digital representation==
 
==Digital representation==
−
As alluded to above, bignums in computer programs are represented using a radix system. This means that a bignum is stored in a base <math>n</math> representation, where the choice of <math>n</math> is based on the application. Precisely, the number <math>N = a_0 + a_1 n + a_2 n^2 + ... + a_k n^k</math> is stored by giving the values <math>a_0, a_1, a_2, ..., a_k</math>, which we probably want to store as an array. Here are a few common possibilities:
+
As alluded to above, bignums in computer programs are represented using a radix system. This means that a bignum is stored in a base <math>n</math> representation, where the choice of <math>n</math> is based on the application. Precisely, the number <math>N = a_0 + a_1 n + a_2 n^2 + ... + a_k n^k</math> is stored by giving the values <math>a_0, a_1, a_2, ..., a_k</math>, which we probably want to store as an array. Here are a few common possibilities, demonstrated for the example of 30! = 265252859812191058636308480000000:
 
* If we let the radix be 10:
 
* If we let the radix be 10:
−
:* ASCII representation: the number is represented by a string which literally contains the number's digits as characters: 265252859812191058636308480000000 would be represented ['2','6','5',...]
+
:* ASCII representation: the number is represented by a string which literally contains the number's digits as characters: 265252859812191058636308480000000 would be represented ['2','6','5',...,'0']
−
:* BCD representation: an array of digits (not their ASCII values), hence [2,6,5,...]
+
:* BCD representation: an array of digits (not their ASCII values), hence [2,6,5,...,0]
 
* If we let the radix be 10<sup>9</sup>, we can store nine digits in each array entry. For example, 30! could be stored [265252,859812191,058636308,480000000]. ''Note that we must take care to group digits starting from the ones' place and moving left'', instead of starting at the most significant digit and moving right, to avoid complicating the code and eroding performance. This is because adding and subtracting bignums requires that they be aligned at the decimal point (not at the most significant digit), so it is convenient when we guarantee that this is never found ''within'' an entry, otherwise shifting would be necessary.
 
* If we let the radix be 10<sup>9</sup>, we can store nine digits in each array entry. For example, 30! could be stored [265252,859812191,058636308,480000000]. ''Note that we must take care to group digits starting from the ones' place and moving left'', instead of starting at the most significant digit and moving right, to avoid complicating the code and eroding performance. This is because adding and subtracting bignums requires that they be aligned at the decimal point (not at the most significant digit), so it is convenient when we guarantee that this is never found ''within'' an entry, otherwise shifting would be necessary.
−
* If we let the radix be 2<sup>32</sup>, we use a sequence of 32-bit unsigned integer typed variables to store the bignum. We know 265252859812191058636308480000000<sub>10</sub> = D13F6370F96865DF5DD54000000<sub>16</sub>. Again, we align at the ones' place, giving [00000D13,F6370F96,865DF5DD,54000000]. (Note that even though the hex representation is given here, internally each element of the array should be stored simply as an integer type.)
+
* If we let the radix be 2<sup>32</sup>, we use a sequence of 32-bit unsigned integer typed variables to store the bignum. We know {{radix|265252859812191058636308480000000|10}} = {{hex|D13F6370F96865DF5DD54000000}}. Again, we align at the ones' place, giving [{{hex|00000D13}},{{hex|F6370F96}},{{hex|865DF5DD}},{{hex|54000000}}]. (Of course, you should not actually explicitly store the hex representations, because that would be cumbersome and slow. It's just an array of 32-bit values.)
 +
 
 +
==Little-endian vs. big-endian==
 +
The ''byte'' is the fundamental addressable unit of memory for a given processor. This is distinct from the ''word'', which is the natural unit of data for a given processor. For example, the Intel 386 processor had 8 bits to a byte but 32 bits to a word. Each byte in memory may be addressed individually by a pointer, but one cannot address the individual bits in them. That being said, when a 32-bit machine word is written to memory, there are two ways it could be done. Suppose the number {{hex|CAFEBABE}} is stored at memory location {{hex|DEADBEEF}}. This will occupy four bytes of memory, and they must be contiguous so that the processor can read and write them as units. The important question is whether the most significant byte (in this case {{hex|CA}}) comes first (big-endian) or last (little-endian). The following table shows where each byte ends up in each scheme.
 +
{|style="border-collapse: collapse; border-width: 1px; border-style: solid; border-color: #000"
 +
! style="border-style: solid; border-width: 1px" |
 +
! style="border-style: solid; border-width: 1px" | {{hex|DEADBEEF}}
 +
! style="border-style: solid; border-width: 1px" | {{hex|DEADBEF0}}
 +
! style="border-style: solid; border-width: 1px" | {{hex|DEADBEF1}}
 +
! style="border-style: solid; border-width: 1px" | {{hex|DEADBEF2}}
 +
|-
 +
| style="border-style: solid; border-width: 1px" | '''Big-endian'''
 +
| style="border-style: solid; border-width: 1px" | {{hex|CA}}
 +
| style="border-style: solid; border-width: 1px" | {{hex|FE}}
 +
| style="border-style: solid; border-width: 1px" | {{hex|BA}}
 +
| style="border-style: solid; border-width: 1px" | {{hex|16}}
 +
|-
 +
| style="border-style: solid; border-width: 1px" | '''Little-endian'''
 +
| style="border-style: solid; border-width: 1px" | {{hex|BE}}
 +
| style="border-style: solid; border-width: 1px" | {{hex|BA}}
 +
| style="border-style: solid; border-width: 1px" | {{hex|FE}}
 +
| style="border-style: solid; border-width: 1px" | {{hex|CA}}
 +
|}
 +
One faces a similar choice when storing bignums: does the most significant part get stored in the first or the last position of the array? Almost every processor is either consistently little-endian or consistently big-endian, but this does not affect the programmer's ability to choose either little-endian or big-endian representations for bignums as the application requires. The importance of this is discussed in the next section.
  
 
==Fixed versus dynamic bignums==
 
==Fixed versus dynamic bignums==
−
There are, in principle, two kinds of bignum implementation. Suppose we know in advance the maximum size of the integers we might be working with. For example, in {{SPOJ|TREE1|TREE1@SPOJ}}, we are asked to report the number of permutations which satisfy a certain property. There are only up to 30 elements, so we know that the answer will not exceed 30! = 265252859812191058636308480000000, which has 33 digits. It is not terribly difficult to implement the solution in such a way that no intermediate variable is ever larger than this. So we could, for example, use a string of length 33 to store all integers used in the computation of the answer (where numbers with fewer than 33 digits are padded with zeroes on the left), and treat all numbers as though they had 33 digits. This is probably the easiest type of bignum to implement.
+
There are, in principle, two kinds of bignum implementation. Suppose we know in advance the maximum size of the integers we might be working with. For example, in {{SPOJ|TREE1|TREE1@SPOJ}}, we are asked to report the number of permutations which satisfy a certain property. There are only up to 30 elements, so we know that the answer will not exceed 30! = 265252859812191058636308480000000, which has 33 digits. It is not terribly difficult to implement the solution in such a way that no intermediate variable is ever larger than this. So we could, for example, use a string of length 33 to store all integers used in the computation of the answer (where numbers with fewer than 33 digits are padded with zeroes on the left), and treat all numbers as though they had 33 digits. The only time when we would care how many digits the number actually has is when outputting it. Addition can now be implemented as a loop over 33 columns, and is fairly simple.
  
−
On the other hand, sometimes it is not so easy to determine in advance the size of the numbers we might be working with, or a problem might have bundled test cases and a strict time limit, forcing the programmer to make the small cases run more quickly than the large ones. When this occurs it is a better idea to use dynamic bignums, which can expand or shrink according to their length. Dynamic bignums are trickier to code than fixed ones. Because extensible array data structures such as C++'s <code>std::vector</code> often support efficient insertion at the back but unacceptable linear-time performance on insertion at the front, it is advisable to store dynamic bignums in little-endian format or ''backward'' (see next section)
+
On the other hand, sometimes it is not so easy to determine in advance the size of the numbers we might be working with, or a problem might have bundled test cases and a strict time limit, forcing the programmer to make the small cases run more quickly than the large ones. When this occurs it is a better idea to use dynamic bignums, which can expand or shrink according to their length. Dynamic bignums are trickier to code than fixed ones: when we add them, for example, we have to take into account that they might not be of the same length; we might then treat all the missing digits as zeroes, but in any case it requires extra code. When using dynamic bignums the difference between the little-endian and big-endian representations becomes significant. If we store the bignums little-endian, and add them, alignment is free: just look at the first entry in each of them; they are in the ones' places of their respective numbers. The code presented in this article will assume the little-endian representation.

Revision as of 01:39, 2 October 2010

Big numbers, known colloquially as bignums (adjectival form bignum, as in bignum arithmetic) are integers whose range exceeds those of machine registers. For example, most modern processors possess 64-bit registers which can be used to store integers up to 264-1. It is usually possible to add, subtract, multiply, or divide such integers in a single machine instruction. However, such machines possess no native implementation of arithmetic on numbers larger than this, nor any native means of representing them. In some applications, it might be necessary to work with numbers with hundreds or even thousands of digits.

Of course, humans have no problems with working with numbers greater than 264-1, other than the fact that it becomes increasingly tedious as the numbers grow larger; we just write them out and use the same algorithms we use on smaller numbers: add column-by-column and carry, and so on. This turns out to be the key to working with bignums in computer programs too. When we write out a number in decimal representation, we are essentially expressing it as a string or array of digits and the algorithms we use to perform arithmetic on them, which entail examining the digits in a particular order, may be considered as loops.

Digital representation

As alluded to above, bignums in computer programs are represented using a radix system. This means that a bignum is stored in a base 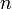n representation, where the choice of 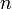n is based on the application. Precisely, the number 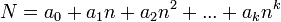N = a_0 + a_1 n + a_2 n^2 + ... + a_k n^k is stored by giving the values 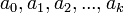a_0, a_1, a_2, ..., a_k, which we probably want to store as an array. Here are a few common possibilities, demonstrated for the example of 30! = 265252859812191058636308480000000:

  • If we let the radix be 10:
  • ASCII representation: the number is represented by a string which literally contains the number's digits as characters: 265252859812191058636308480000000 would be represented ['2','6','5',...,'0']
  • BCD representation: an array of digits (not their ASCII values), hence [2,6,5,...,0]
  • If we let the radix be 109, we can store nine digits in each array entry. For example, 30! could be stored [265252,859812191,058636308,480000000]. Note that we must take care to group digits starting from the ones' place and moving left, instead of starting at the most significant digit and moving right, to avoid complicating the code and eroding performance. This is because adding and subtracting bignums requires that they be aligned at the decimal point (not at the most significant digit), so it is convenient when we guarantee that this is never found within an entry, otherwise shifting would be necessary.
  • If we let the radix be 232, we use a sequence of 32-bit unsigned integer typed variables to store the bignum. We know 26525285981219105863630848000000010 = D13F6370F96865DF5DD5400000016. Again, we align at the ones' place, giving [00000D1316,F6370F9616,865DF5DD16,5400000016]. (Of course, you should not actually explicitly store the hex representations, because that would be cumbersome and slow. It's just an array of 32-bit values.)

Little-endian vs. big-endian

The byte is the fundamental addressable unit of memory for a given processor. This is distinct from the word, which is the natural unit of data for a given processor. For example, the Intel 386 processor had 8 bits to a byte but 32 bits to a word. Each byte in memory may be addressed individually by a pointer, but one cannot address the individual bits in them. That being said, when a 32-bit machine word is written to memory, there are two ways it could be done. Suppose the number CAFEBABE16 is stored at memory location DEADBEEF16. This will occupy four bytes of memory, and they must be contiguous so that the processor can read and write them as units. The important question is whether the most significant byte (in this case CA16) comes first (big-endian) or last (little-endian). The following table shows where each byte ends up in each scheme.

DEADBEEF16 DEADBEF016 DEADBEF116 DEADBEF216
Big-endian CA16 FE16 BA16 1616
Little-endian BE16 BA16 FE16 CA16

One faces a similar choice when storing bignums: does the most significant part get stored in the first or the last position of the array? Almost every processor is either consistently little-endian or consistently big-endian, but this does not affect the programmer's ability to choose either little-endian or big-endian representations for bignums as the application requires. The importance of this is discussed in the next section.

Fixed versus dynamic bignums

There are, in principle, two kinds of bignum implementation. Suppose we know in advance the maximum size of the integers we might be working with. For example, in TREE1@SPOJ, we are asked to report the number of permutations which satisfy a certain property. There are only up to 30 elements, so we know that the answer will not exceed 30! = 265252859812191058636308480000000, which has 33 digits. It is not terribly difficult to implement the solution in such a way that no intermediate variable is ever larger than this. So we could, for example, use a string of length 33 to store all integers used in the computation of the answer (where numbers with fewer than 33 digits are padded with zeroes on the left), and treat all numbers as though they had 33 digits. The only time when we would care how many digits the number actually has is when outputting it. Addition can now be implemented as a loop over 33 columns, and is fairly simple.

On the other hand, sometimes it is not so easy to determine in advance the size of the numbers we might be working with, or a problem might have bundled test cases and a strict time limit, forcing the programmer to make the small cases run more quickly than the large ones. When this occurs it is a better idea to use dynamic bignums, which can expand or shrink according to their length. Dynamic bignums are trickier to code than fixed ones: when we add them, for example, we have to take into account that they might not be of the same length; we might then treat all the missing digits as zeroes, but in any case it requires extra code. When using dynamic bignums the difference between the little-endian and big-endian representations becomes significant. If we store the bignums little-endian, and add them, alignment is free: just look at the first entry in each of them; they are in the ones' places of their respective numbers. The code presented in this article will assume the little-endian representation.

Retrieved from "https://wcipeg.com/wiki/index.php?title=Big_numbers&oldid=472"