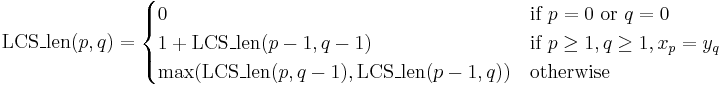Longest common subsequence
The longest common subsequence (LCS) problem is the problem of finding a sequence of maximal length that is a subsequence of two finite input sequences. Formally, given two sequences ![x = [x_1, x_2, ..., x_m]](/wiki/images/math/1/7/e/17e3b809608df816ca3f2fcd01567bd0.png) and
and ![y = [y_1, y_2, ..., y_n]](/wiki/images/math/a/5/3/a5338e19800ecd53871d29546df721a3.png) , we would like to find two sets of indices
, we would like to find two sets of indices 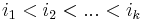 and
and 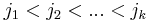 such that
such that 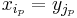 for all
for all 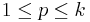 and
and  is maximized.
is maximized.
Contents
Discussion
Two strings may have a potentially exponential number of longest common subsequences. An example (with proof) is given here (take the string given and its reverse as the input sequences). Therefore, it is clear that any algorithm to return all longest common subsequences of a pair of input sequences (i.e., all possible sequences  and
and  of indices as previously defined) cannot run in polynomial time.
of indices as previously defined) cannot run in polynomial time.
If, however, we restrict ourselves to either reporting simply the maximum value of  or reporting only one possible pair of sequences
or reporting only one possible pair of sequences 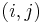 for which the maximum
for which the maximum  is achieved, then the problem may be solved in polynomial time using dynamic programming.
is achieved, then the problem may be solved in polynomial time using dynamic programming.
Algorithm
Optimal substructure
Consider the structure of an optimal solution. (That is, one of possibly many optimal solutions; we don't care which one we're looking for.) We want to show that this problem has the optimal substructure required for a dynamic solution. To do this, we first notice that our optimal solution either uses or does not use the last element of  , and either uses or does not use the last element of
, and either uses or does not use the last element of  . And then we make these two critical observations:
. And then we make these two critical observations:
- If a longest common subsequence of
 and
and  does not use the last term of
does not use the last term of  or does not use the last term of
or does not use the last term of  (or both), then we can drop the unused terms from the end of
(or both), then we can drop the unused terms from the end of  and
and  and our longest common subsequence will be a longest common subsequence of the shortened sequences. That is, the optimal solution contains an optimal solution to a smaller problem.
and our longest common subsequence will be a longest common subsequence of the shortened sequences. That is, the optimal solution contains an optimal solution to a smaller problem.
- Why is this true? Clearly the longest common subsequence of
 and
and  is at least some common subsequence of the shortened sequences, because we didn't cut off any terms we used. So the longest common subsequence of the shortened sequences is at least as long as the longest common subsequence of
is at least some common subsequence of the shortened sequences, because we didn't cut off any terms we used. So the longest common subsequence of the shortened sequences is at least as long as the longest common subsequence of  and
and  . Could it be longer? No, because then we could just add back in those terms we chopped off from the end, and get a common subsequence of
. Could it be longer? No, because then we could just add back in those terms we chopped off from the end, and get a common subsequence of  and
and  longer than what we originally assumed was the maximum length --- a contradiction.
longer than what we originally assumed was the maximum length --- a contradiction.
- Why is this true? Clearly the longest common subsequence of
- If a longest common subsequence of
 and
and  uses the last term of
uses the last term of  and the last term of
and the last term of  , then we can drop the last term from both
, then we can drop the last term from both  and
and  as well as the last term from our common subsequence and we will be left with a common subsequence of the shortened
as well as the last term from our common subsequence and we will be left with a common subsequence of the shortened  and
and  .
.
- Similar reasoning applies here: if the shortened common subsequence were not optimal, adding back in the common last term would give a better-than-optimal solution to the original problem.
It follows that if a longest common subsequence of  and
and  uses the last element of both
uses the last element of both  and
and  , then its length is one more than that of some longest common subsequence of
, then its length is one more than that of some longest common subsequence of  lacking its last element and
lacking its last element and  lacking its last element. If it does not, then its length is exactly the same as that of some longest common subsequence of the shortened
lacking its last element. If it does not, then its length is exactly the same as that of some longest common subsequence of the shortened  and
and  (one or both may be shortened).
(one or both may be shortened).
Here is an example. A longest common subsequence of the sequences ![[9,2,3,6]](/wiki/images/math/b/5/a/b5ae5a9c8f78a50e1e32615df6d5e282.png) and
and ![[2,0,6,3]](/wiki/images/math/e/3/3/e33b6bb07db92901351ccfc7b250804d.png) is
is ![[2,3]](/wiki/images/math/d/5/1/d5138fec13c27bb6c645b29cdfa97a84.png) . (
. (![[2,6]](/wiki/images/math/0/1/1/0115a0c32df0c9878381ac50ee93eefd.png) would also work.) This common subsequence uses the last element of the second sequence but it does not use the last element of the first sequence. Therefore, we can drop the last element of the first sequence, and conclude that
would also work.) This common subsequence uses the last element of the second sequence but it does not use the last element of the first sequence. Therefore, we can drop the last element of the first sequence, and conclude that ![[2,3]](/wiki/images/math/d/5/1/d5138fec13c27bb6c645b29cdfa97a84.png) is also a longest common subsequence of
is also a longest common subsequence of ![[9,2,3]](/wiki/images/math/b/d/0/bd01f349b4fc967b2136924cc423104e.png) and
and ![[2,0,6,3]](/wiki/images/math/e/3/3/e33b6bb07db92901351ccfc7b250804d.png) . Notice that in this subproblem, the last elements of both sequences are used. Now we know that we can drop the last elements of both sequences as well as the last element of our longest common subsequence;
. Notice that in this subproblem, the last elements of both sequences are used. Now we know that we can drop the last elements of both sequences as well as the last element of our longest common subsequence; ![[2]](/wiki/images/math/b/e/b/beb4dbf9af069aa2df7b147229965085.png) must be a longest common subsequence of
must be a longest common subsequence of ![[9,2]](/wiki/images/math/e/4/d/e4d830bf7280ee64ce69250c7fadb25c.png) and
and ![[2,0,6]](/wiki/images/math/6/b/b/6bbeacdb35bd67260aa80a3a467766ea.png) , and indeed it is.
, and indeed it is.
Since an optimal solution to a general instance of the longest common subsequence problem contains optimal solutions to subinstances, we can reconstruct the optimal solution to the original instance once we know the optimal solutions to all subinstances, i.e., work forward, thus:
- If the last element of
 and the last element of
and the last element of  are the same, then some longest common subsequence of the two uses the last element of both sequences, and, furthermore, any longest common subsequence of
are the same, then some longest common subsequence of the two uses the last element of both sequences, and, furthermore, any longest common subsequence of 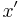 and
and 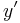 (i.e.,
(i.e.,  and
and  with their last elements removed) can be turned into a longest common subsequence of
with their last elements removed) can be turned into a longest common subsequence of  and
and  .
.
- Why? It would be absurd to use the last element of neither sequence, as we could just append that last element onto the end of a supposedly optimal common subsequence to obtain a longer one. For example, the sequence
![[9,2]](/wiki/images/math/e/4/d/e4d830bf7280ee64ce69250c7fadb25c.png) cannot possibly be a longest common subsequence of
cannot possibly be a longest common subsequence of ![[9,2,3,6]](/wiki/images/math/b/5/a/b5ae5a9c8f78a50e1e32615df6d5e282.png) and
and ![[3,9,2,6]](/wiki/images/math/b/4/c/b4c24fe5e3c624123317c3fa9b6aa05c.png) because it fails to use the 6; clearly
because it fails to use the 6; clearly ![[9,2,6]](/wiki/images/math/0/e/1/0e186b639e938027d9d48a1313f04df4.png) is a longer common subsequence. Furthermore, if we use the last element of only one of the sequences, and it is matched to some element other than the last in the other sequence, we can substitute it with the last instead. For example, it may be true that selecting the nine and the first six from
is a longer common subsequence. Furthermore, if we use the last element of only one of the sequences, and it is matched to some element other than the last in the other sequence, we can substitute it with the last instead. For example, it may be true that selecting the nine and the first six from ![[9,2,6,6]](/wiki/images/math/3/2/7/327773dc2103b65e6244f5dd2f06692d.png) and selecting the nine and six from
and selecting the nine and six from ![[9,6]](/wiki/images/math/1/c/f/1cff4a4498f7f6beb070ee16b2711935.png) gives a longest common subsequence of
gives a longest common subsequence of ![[9,2,6,6]](/wiki/images/math/3/2/7/327773dc2103b65e6244f5dd2f06692d.png) and
and ![[9,6]](/wiki/images/math/1/c/f/1cff4a4498f7f6beb070ee16b2711935.png) , but it is also true that we could have just as well selected the second six from
, but it is also true that we could have just as well selected the second six from ![[9,2,6,6]](/wiki/images/math/3/2/7/327773dc2103b65e6244f5dd2f06692d.png) , hence using the last element of both sequences.
, hence using the last element of both sequences.
- Why? It would be absurd to use the last element of neither sequence, as we could just append that last element onto the end of a supposedly optimal common subsequence to obtain a longer one. For example, the sequence
- If the last element of
 and the last element of
and the last element of  differ, then some longest common subsequence of the two is either a longest common subsequence of
differ, then some longest common subsequence of the two is either a longest common subsequence of 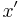 and
and  or of
or of  and
and 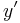 , and, furthermore, it doesn't matter which longest common subsequences of
, and, furthermore, it doesn't matter which longest common subsequences of 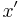 and
and  and of
and of  and
and 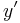 we know; one of them will be a longest common subsequence for
we know; one of them will be a longest common subsequence for  and
and  .
.
- Since the last elements of
 and
and  differ, obviously there is no longest common subsequence that uses both of them. Thus we can always remove either the last element of
differ, obviously there is no longest common subsequence that uses both of them. Thus we can always remove either the last element of  or the last element of
or the last element of  . For example, some longest common subsequence of
. For example, some longest common subsequence of ![[9,2,3,6,1]](/wiki/images/math/2/3/b/23b0362d5d775431573aff1f9a79ecb0.png) and
and ![[2,0,6,1,3]](/wiki/images/math/4/5/f/45f3c361453ff90fe499902ae5965332.png) should be found if we consider a longest common subsequence of
should be found if we consider a longest common subsequence of ![[9,2,3,6]](/wiki/images/math/b/5/a/b5ae5a9c8f78a50e1e32615df6d5e282.png) and
and ![[2,0,6,1,3]](/wiki/images/math/4/5/f/45f3c361453ff90fe499902ae5965332.png) and of
and of ![[9,2,3,6,1]](/wiki/images/math/2/3/b/23b0362d5d775431573aff1f9a79ecb0.png) and
and ![[2,0,6,1]](/wiki/images/math/5/f/6/5f62da4e554a53f13bf06022a1b67117.png) . This is indeed the case;
. This is indeed the case; ![[2,3]](/wiki/images/math/d/5/1/d5138fec13c27bb6c645b29cdfa97a84.png) is a longest common subsequence of the first pair and
is a longest common subsequence of the first pair and ![[2,6,1]](/wiki/images/math/7/a/7/7a7b8ea476b40eac3796f2e004c990de.png) is a longest common subsequence of the second pair, and
is a longest common subsequence of the second pair, and ![[2,6,1]](/wiki/images/math/7/a/7/7a7b8ea476b40eac3796f2e004c990de.png) , the longer of the two, is also a longest common subsequence of
, the longer of the two, is also a longest common subsequence of ![[9,2,3,6,1]](/wiki/images/math/2/3/b/23b0362d5d775431573aff1f9a79ecb0.png) and
and ![[2,0,6,1,3]](/wiki/images/math/4/5/f/45f3c361453ff90fe499902ae5965332.png) .
.
- Since the last elements of
Overlapping subproblems and state
As explained in the preceding section, the solution to an instance of the longest common subsequence problem depends on the solutions to subinstances, which are formed by removing the last element from either or both of the input sequences. In order to obtain an efficient dynamic programming solution, we want the total number of possible subinstances, subinstances of subinstances, and so on down to be bounded polynomially. Is this true?
Luckily, it is. The only subinstances we have to consider are those in which the two input sequences are both prefixes of the two given sequences. There are 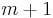 prefixes of
prefixes of  and
and 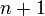 prefixes of
prefixes of  , so there are only
, so there are only 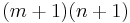 subinstances to consider in total.
subinstances to consider in total.
We see that our dynamic state only needs to consist of two values 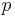 and
and 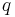 , used to uniquely identify the subinstance consisting of the first
, used to uniquely identify the subinstance consisting of the first 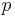 elements of
elements of  and the first
and the first 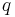 elements of
elements of  .
.
Base case
A simple base case is that if one of the input sequences is empty, then the longest common subsequence is also empty (as the empty sequence is the only subsequence of the empty sequence). This base case complements our optimal substructure nicely, since it accounts for when it is no longer possible to remove the last element.
Putting it together
Here, then, is a recursive function to compute the longest common subsequence:
Notice that in the second case, we are concatenating the common last element to the end of a longest common subsequence of the prefixes shortened by one element, and in the third case, if there is a tie in length, we don't care which one we take.
Since the value of this recursive function depends only on the values of the function called with arguments that are less than or equal to the original arguments, we can compute all values of 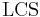 bottom-up by looping
bottom-up by looping 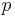 from 0 to
from 0 to 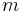 and looping
and looping 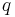 from 0 to
from 0 to  .
.
If only the lengths are desired:
Finally, the solution to the original instance is either 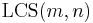 or
or 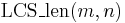 , whichever is desired; here we are solving the problem for the entire input sequences.
, whichever is desired; here we are solving the problem for the entire input sequences.
Analysis
Time
The function 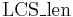 defined above takes constant time to transition from one state to another, and there are
defined above takes constant time to transition from one state to another, and there are 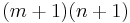 states, so the time taken overall is
states, so the time taken overall is 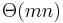 .
.
The function 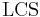 as written above may take longer to compute if we naively store an array of strings where each entry is the longest common subsequence of some subinstance, because then a lot of string copying occurs during transitions, and this presumably takes more than constant time. If we actually wish to reconstruct a longest common subsequence, we may compute the
as written above may take longer to compute if we naively store an array of strings where each entry is the longest common subsequence of some subinstance, because then a lot of string copying occurs during transitions, and this presumably takes more than constant time. If we actually wish to reconstruct a longest common subsequence, we may compute the 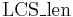 table first, making a note of "what happened" when each value was computed (\emph{i.e.}, which subinstance's solution was used) and then backtrack once
table first, making a note of "what happened" when each value was computed (\emph{i.e.}, which subinstance's solution was used) and then backtrack once 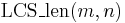 is known. This then also takes
is known. This then also takes 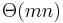 time.
time.
Using the recursive definition of 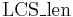 as written may be faster (provided memoization is used), because we may not have to compute all values that we would compute in the dynamic solution. The runtime is then
as written may be faster (provided memoization is used), because we may not have to compute all values that we would compute in the dynamic solution. The runtime is then 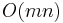 (no improvement is seen in the worst case).
(no improvement is seen in the worst case).
In the dynamic solution, if we desire only the length of the LCS, we notice that we only need to keep two rows of the table at any given time, since we will never be looking back at  -values less than the current
-values less than the current  minus one. In fact, keeping only two rows at any given time may be more cache-optimal, and hence result in a constant speedup.
minus one. In fact, keeping only two rows at any given time may be more cache-optimal, and hence result in a constant speedup.
Memory
The memory usage is 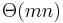 for the dynamic solution. The recursive solution may use less memory if hashing techniques are used to implement memoization.
for the dynamic solution. The recursive solution may use less memory if hashing techniques are used to implement memoization.
Alternative formulation
Here is another way of thinking about the longest common subsequence problem. Draw a table and place the elements of  along the left and the elements of
along the left and the elements of  across the top of the table, so that there is one entry in the table for every pair of elements from
across the top of the table, so that there is one entry in the table for every pair of elements from  and
and  . Place a checkmark in any box where the row element and the column element match. For example:
. Place a checkmark in any box where the row element and the column element match. For example:
| 9 | 2 | 3 | 6 | 1 | |
|---|---|---|---|---|---|
| 2 | ✓ | ||||
| 0 | |||||
| 6 | ✓ | ||||
| 1 | ✓ | ||||
| 3 | ✓ |
Any sequence of checkmarks such that each one is strictly below and to the right of the previous one is a common subsequence. We want as long a sequence as possible; this will be a longest common subsequence. It should be clear from looking at the table above that ![[2,6,1]](/wiki/images/math/7/a/7/7a7b8ea476b40eac3796f2e004c990de.png) is the desired longest common subsequence. Our DP table can be understood as follows:
is the desired longest common subsequence. Our DP table can be understood as follows: 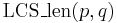 is the best we can do given that we only use checkmarks from the first
is the best we can do given that we only use checkmarks from the first 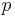 rows and the first
rows and the first 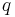 columns. The condition
columns. The condition 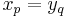 corresponds to the case in which there is a checkmark in the box at
corresponds to the case in which there is a checkmark in the box at 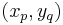 .
.
Faster methods
The dynamic algorithm presented above always takes the same amount of time to run (to within a constant factor) and it does not depend on the size of the set from which the elements of the sequences are taken. Faster algorithms exist for cases where this set is small and finite (making the sequences strings over a relatively small alphabet), one of the strings is much longer than the other, or the two strings are very similar.[1] These algorithms almost always outperform the naive algorithm in practice (otherwise the diff utility would be unacceptably slow). However, it is surprisingly difficult to improve over the 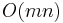 bound of this algorithm in the general case.
bound of this algorithm in the general case.
References
- ↑ L. Bergroth and H. Hakonen and T. Raita (2000). "A Survey of Longest Common Subsequence Algorithms". SPIRE (IEEE Computer Society) 00: 39–48. doi:10.1109/SPIRE.2000.878178. ISBN 0-7695-0746-8.
![\operatorname{LCS}(p,q) =
\begin{cases}
[\,] & \text{if } p=0 \text{ or } q=0 \\
(\operatorname{LCS}(p-1,q-1))x_p & \text{if } p\geq 1, q \geq 1, x_p = y_q \\
\text{the longer of }\operatorname{LCS}(p,q-1)\text{ and }\operatorname{LCS}(p-1,q) & \text{otherwise}
\end{cases}](/wiki/images/math/d/5/a/d5a3df9831990cfadc44237dc5abd77c.png)