Longest increasing subsequence
The longest increasing subsequence (LIS) problem is to find an increasing subsequence (either strictly or non-strictly) of maximum length, given an input sequence whose elements belong are taken from a partially ordered set. For example, consider the sequence [9,2,6,3,1,5,0,7]. An increasing subsequence is [2,3,5,7], and, in fact, there is no longer increasing subsequence. Therefore [2,3,5,7] is a longest increasing subsequence of [9,2,6,3,1,5,0,7]. The longest decreasing subsequence can be defined analogously; it is clear that a solution to one gives a solution to the other.
Contents
Discussion
There are three possible ways to state the problem:
- Return all longest increasing subsequences. There may be an exponential number of these; for example, consider a sequence that starts [1,0,3,2,5,4,7,6,...]; if it has length
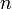 (even) then there are
(even) then there are 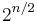 increasing subsequences of length
increasing subsequences of length 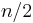 (each obtained by choosing one out of each of the pairs (1,0), (3,2), ...), and no longer increasing subsequences. Thus, this problem cannot possibly be solved efficiently.
(each obtained by choosing one out of each of the pairs (1,0), (3,2), ...), and no longer increasing subsequences. Thus, this problem cannot possibly be solved efficiently. - Return one longest increasing subsequence. This can be solved efficiently.
- Return only the maximum length that a increasing subsequence can have. This can be solved efficiently.
Reduction to LCS from non-strict case
Any increasing subsequence of a sequence is also a subsequence of the sequence sorted. For example, [9,2,6,3,1,5,0,7], when sorted, gives [0,1,2,3,5,6,7,9], and [2,3,5,7] is certainly a subsequence of this. Furthermore, if a subsequence of the original sequence is also a subsequence of the sorted sequence, then clearly it is increasing (non-strictly), and therefore an increasing subsequence of the original sequence. It follows trivially that we can compute a longest non-strictly increasing subsequence by computing a longest common subsequence of the sequence and a sorted copy of itself.
Dynamic programming solution
To compute the longest increasing subsequence contained with a given sequence ![x = [x_1, x_2, ..., x_n]](/wiki/images/math/6/2/1/621e79c67b0b6441801885ad6a9e6bbd.png) , first notice that unless
, first notice that unless  is empty, an LIS will have length at least one, and given that this is the case, it has some last element
is empty, an LIS will have length at least one, and given that this is the case, it has some last element 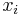 . Denote the (non-empty) prefixes of
. Denote the (non-empty) prefixes of  by
by ![x[1] = [x_1], x[2] = [x_1, x_2], ..., x[n] = x](/wiki/images/math/2/3/9/2396e4d2839ee5d54d6aa9dfc7b04487.png) . Then, an LIS that ends with element
. Then, an LIS that ends with element 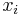 has the property that it is an LIS that uses the last element of
has the property that it is an LIS that uses the last element of ![x[i]](/wiki/images/math/e/c/a/eca9bd72b911b96661e70a7bf689d0ca.png) . Thus, for each of the prefixes
. Thus, for each of the prefixes ![x[1], x[2], ..., x[n]](/wiki/images/math/4/1/6/416c6a38c37b23141c0aae1eef870e46.png) , we will determine an increasing subsequence that contains the last element of this prefix sequence such that no longer increasing subsequence has this property. Then, one of these must be a LIS for the original sequence.
, we will determine an increasing subsequence that contains the last element of this prefix sequence such that no longer increasing subsequence has this property. Then, one of these must be a LIS for the original sequence.
For example, consider the sequence [9,2,6,3,1,5,0]. Its nonempty prefixes are [9], [9,2], [9,2,6], [9,2,6,3], [9,2,6,3,1], [9,2,6,3,1,5], and [9,2,6,3,1,5,0]. For each of these, we may find an increasing subsequence that uses the last element of maximal length, for example, [9], [2], [2,6], [2,3], [1], [2,3,5], and [0], respectively. The longest of these, [2,3,5], is then also an (unrestricted) LIS of the original sequence, [9,2,6,3,1,5,0,7].
Denote the LIS of  by
by 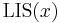 , and denote the LIS subject to the restriction that the last element must be used as
, and denote the LIS subject to the restriction that the last element must be used as ![\operatorname{LIS}'(x[i])](/wiki/images/math/a/0/9/a09ea6dcfead478b0b4ac6bb0a096a3b.png) . Then we see that
. Then we see that ![|\operatorname{LIS}(x)| = \max_{1 \leq i \leq n} |\operatorname{LIS}'(x[i])|](/wiki/images/math/3/7/7/37794c0ee66e331d9d4cb261412ab248.png) . We will now focus on calculating the
. We will now focus on calculating the 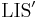 values, of which there are
values, of which there are 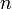 (one for each nonempty prefix of
(one for each nonempty prefix of  ).
).