Least common multiple
The least common multiple (LCM) of a set of integers is the least positive integer that is a multiple of all the integers in the set, unless one of the integers is zero, in which case the LCM is defined to be zero. For example, the LCM of 6 and 8 is 24, because 24 is a multiple of 6 and 8, and no smaller positive integer has this property. The LCM is also known as the lowest common multiple. Because finding the LCM is the first step of adding two reduced fractions (so they can be put under a common denominator), finding the LCM is also referred to as finding the lowest common denominator or least common denominator (LCD).
Properties
-
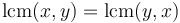 (commutativity)
(commutativity) -
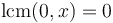
-
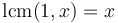
-
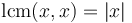
- The multiples of the LCM constitute the entire set of common multiples of a given set of integers. For example, the LCM of 6 and 8 is 24, and the entire set of common multiples of 6 and 8 is
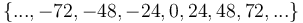 ; notice that all these numbers are multiples of the LCM, 24.
; notice that all these numbers are multiples of the LCM, 24. - The LCM is never negative, because if
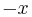 is a common multiple, then so is
is a common multiple, then so is 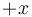 . Also,
. Also, 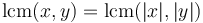 .
. - If
 and
and  are sets, then
are sets, then 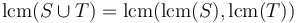 . For example,
. For example, 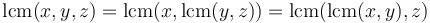 (associativity).
(associativity). -
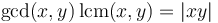 .
. -
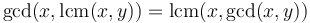 . (This property is the absorption law of the lattice over the positive integers with GCD as meet and LCM as join.)
. (This property is the absorption law of the lattice over the positive integers with GCD as meet and LCM as join.) - If
 has prime factorization
has prime factorization 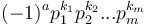 and
and 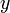 has prime factorization
has prime factorization 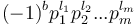 , then
, then 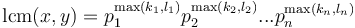 . Therefore, it is possible to find the LCM of two integers by factorizing them; but much more efficient methods exist.
. Therefore, it is possible to find the LCM of two integers by factorizing them; but much more efficient methods exist. -
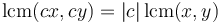 whenever
whenever 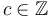 .
.
Calculation
The LCM is calculated using the property above that 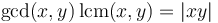 ; efficient algorithms are known for computing the greatest common divisor. Hence:
; efficient algorithms are known for computing the greatest common divisor. Hence:
int lcm(int x, int y) { if (x == 0 || y == 0) return 0; else return abs(x*y)/gcd(x,y); }
The multiplication step may cause unnecessary overflow (such as when taking the LCM of 106 and 109), so the following is often used instead:
int lcm(int x, int y) { if (x == 0 || y == 0) return 0; else return abs(x/gcd(x,y)*y); }