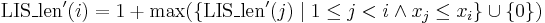Longest increasing subsequence
The longest increasing subsequence (LIS) problem is to find an increasing subsequence (either strictly or non-strictly) of maximum length, given a (finite) input sequence whose elements are taken from a partially ordered set. For example, consider the sequence [9,2,6,3,1,5,0,7]. An increasing subsequence is [2,3,5,7], and, in fact, there is no longer increasing subsequence. Therefore [2,3,5,7] is a longest increasing subsequence of [9,2,6,3,1,5,0,7]. The longest decreasing subsequence can be defined analogously; it is clear that a solution to one gives a solution to the other.
We will focus on the non-strict case (with some parenthetical comments about the strict case).
Contents
Discussion
There are three possible ways to state the problem:
- Return all longest increasing subsequences. There may be an exponential number of these; for example, consider a sequence that starts [1,0,3,2,5,4,7,6,...]; if it has length
 (even) then there are
(even) then there are 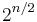 increasing subsequences of length
increasing subsequences of length 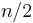 (each obtained by choosing one out of each of the pairs (1,0), (3,2), ...), and no longer increasing subsequences. Thus, this problem cannot possibly be solved efficiently.
(each obtained by choosing one out of each of the pairs (1,0), (3,2), ...), and no longer increasing subsequences. Thus, this problem cannot possibly be solved efficiently. - Return one longest increasing subsequence. This can be solved efficiently.
- Return only the maximum length that a increasing subsequence can have. This can be solved efficiently.
Reduction to LCS from non-strict case
Any increasing subsequence of a sequence is also a subsequence of the sequence sorted. For example, [9,2,6,3,1,5,0,7], when sorted, gives [0,1,2,3,5,6,7,9], and [2,3,5,7] is certainly a subsequence of this. Furthermore, if a subsequence of the original sequence is also a subsequence of the sorted sequence, then clearly it is increasing (non-strictly), and therefore an increasing subsequence of the original sequence. It follows trivially that we can compute a longest non-strictly increasing subsequence by computing a longest common subsequence of the sequence and a sorted copy of itself.
Dynamic programming solution
To compute the longest increasing subsequence contained with a given sequence ![x = [x_1, x_2, ..., x_n]](/wiki/images/math/6/2/1/621e79c67b0b6441801885ad6a9e6bbd.png) , first notice that unless
, first notice that unless  is empty, an LIS will have length at least one, and given that this is the case, it has some last element
is empty, an LIS will have length at least one, and given that this is the case, it has some last element  . Denote the (non-empty) prefixes of
. Denote the (non-empty) prefixes of  by
by ![x[1] = [x_1], x[2] = [x_1, x_2], ..., x[n] = x](/wiki/images/math/2/3/9/2396e4d2839ee5d54d6aa9dfc7b04487.png) . Then, an LIS that ends with element
. Then, an LIS that ends with element  has the property that it is an LIS that uses the last element of
has the property that it is an LIS that uses the last element of ![x[i]](/wiki/images/math/e/c/a/eca9bd72b911b96661e70a7bf689d0ca.png) . Thus, for each of the prefixes
. Thus, for each of the prefixes ![x[1], x[2], ..., x[n]](/wiki/images/math/4/1/6/416c6a38c37b23141c0aae1eef870e46.png) , we will determine an increasing subsequence that contains the last element of this prefix sequence such that no longer increasing subsequence has this property. Then, one of these must be a LIS for the original sequence.
, we will determine an increasing subsequence that contains the last element of this prefix sequence such that no longer increasing subsequence has this property. Then, one of these must be a LIS for the original sequence.
For example, consider the sequence [9,2,6,3,1,5,0]. Its nonempty prefixes are [9], [9,2], [9,2,6], [9,2,6,3], [9,2,6,3,1], [9,2,6,3,1,5], and [9,2,6,3,1,5,0]. For each of these, we may find an increasing subsequence that uses the last element of maximal length, for example, [9], [2], [2,6], [2,3], [1], [2,3,5], and [0], respectively. The longest of these, [2,3,5], is then also an (unrestricted) LIS of the original sequence, [9,2,6,3,1,5,0,7].
Denote the LIS of  by
by 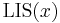 , and denote the LIS subject to the restriction that the last element must be used as
, and denote the LIS subject to the restriction that the last element must be used as 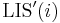 . Then we see that
. Then we see that 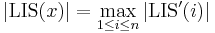 . We will now focus on calculating the
. We will now focus on calculating the 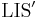 values, of which there are
values, of which there are  (one for each nonempty prefix of
(one for each nonempty prefix of  ).
).
Optimal substructure
The value for 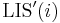 consists of either:
consists of either:
- the element
 alone, which always forms an increasing subsequence by itself, or
alone, which always forms an increasing subsequence by itself, or - the element
 tacked on to the end of an increasing subsequence ending with
tacked on to the end of an increasing subsequence ending with 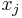 , where
, where 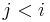 and
and 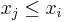 (for the non-strict case) or
(for the non-strict case) or 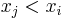 (for the strict case).
(for the strict case).
For example, the longest increasing subsequence that ends on the last element of ![[9,2,6,3,1]](/wiki/images/math/2/8/2/2824ba6a694a1cbb33bcbc4dd0b9845a.png) is just the element
is just the element 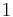 itself, the element at the very end. But if we consider
itself, the element at the very end. But if we consider ![[9,2,6,3,1,5]](/wiki/images/math/3/3/9/33945c6653ad9b9190b8293b38741303.png) , which has as a longest increasing subsequence ending at its last element
, which has as a longest increasing subsequence ending at its last element ![[2,3,5]](/wiki/images/math/3/3/c/33cd7433211350933b73bc316943e6b8.png) , we see that
, we see that ![[2,3]](/wiki/images/math/d/5/1/d5138fec13c27bb6c645b29cdfa97a84.png) is an increasing subsequence of
is an increasing subsequence of ![[9,2,6,3]](/wiki/images/math/8/4/b/84b2b8698c67105233fed595d56323d7.png) ending at its last element and that
ending at its last element and that 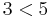 as required.
as required.
Furthermore, it is not hard to see that the increasing subsequence we are left with after removing the last element, in the second case, must itself be optimal for the element it ends on; that is, must be a possible value of 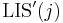 . If this were not the case, then we would have a longer increasing subsequence ending on
. If this were not the case, then we would have a longer increasing subsequence ending on 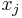 , and then we could tack the element
, and then we could tack the element  on the end to obtain an increasing subsequence ending at
on the end to obtain an increasing subsequence ending at  that is longer than the one we originally supposed was longest --- a contradiction.
that is longer than the one we originally supposed was longest --- a contradiction.
Also, if we already know 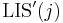 for all
for all 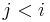 , then one of them, when the element
, then one of them, when the element  is appended to the end, must give a LIS that ends at
is appended to the end, must give a LIS that ends at  , unless
, unless ![\operatorname{LIS}'(x[i])](/wiki/images/math/a/0/9/a09ea6dcfead478b0b4ac6bb0a096a3b.png) consists of
consists of  only. This is because if this were not the case, then whenever we were allowed to append
only. This is because if this were not the case, then whenever we were allowed to append  we would obtain a suboptimal solution --- but then removing the last element from
we would obtain a suboptimal solution --- but then removing the last element from 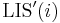 would give a suboptimal solution to a subinstance, which we know to be impossible.
would give a suboptimal solution to a subinstance, which we know to be impossible.
Overlapping subproblems
When computing ![\operatorname{LIS}'(x[i])](/wiki/images/math/a/0/9/a09ea6dcfead478b0b4ac6bb0a096a3b.png) , we might need to know the values of
, we might need to know the values of ![\operatorname{LIS}'(x[j])](/wiki/images/math/2/6/2/2622812a25f0ba36ff5cc6071cf50fa7.png) for all
for all 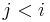 . These are the shared subinstances; there are only
. These are the shared subinstances; there are only  possible values in the
possible values in the 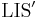 table in total.
table in total.
Implementation
The optimal substructure discussed gives a very simple formula:
(In the strict case, we have 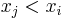 strictly.)
strictly.)
We can easily compute this bottom-up, since we only need to know values of smaller subinstances.
The LIS of the entire sequence  is then just the largest of all
is then just the largest of all 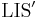 values.
values.
If only the length is desired, the above formula becomes
Pseudocode
(This is for the non-strict case.)
input x
n ← length of x
for each i ∈ [1..n]
lis[i] ← 1
for each j ∈ [1..(i-1)]
if x[i] ≥ x[j]
lis[i] ← max(lis[i],1+lis[j])
return max element of lis
Analysis
Time
With the length-only formula above, computing the 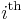 entry takes
entry takes 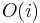 time to compute, giving
time to compute, giving 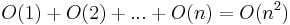 time overall.
time overall.
This bound still holds when computing the LIS itself, but since we probably wish to avoid needless copying and concatenation of sequences, a better way is to, instead of storing the 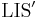 values themselves in the table, simply storing their lengths as well as making a note of the next-to-last element of the sequence (or storing a zero if there is none) so that we can backtrack to reconstruct the original sequence.
values themselves in the table, simply storing their lengths as well as making a note of the next-to-last element of the sequence (or storing a zero if there is none) so that we can backtrack to reconstruct the original sequence.
Memory
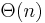 memory is used.
memory is used.
A faster algorithm
If the set from which the elements of  is taken is totally ordered, then we can do even better than this. As a matter of fact, this is usually the case, as the elements will often be integers or real numbers. This algorithm runs in
is taken is totally ordered, then we can do even better than this. As a matter of fact, this is usually the case, as the elements will often be integers or real numbers. This algorithm runs in 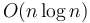 time, which is asymptotically optimal.[1]
time, which is asymptotically optimal.[1]
The idea behind the algorithm is that if an increasing subsequence is long, then it is useful because it might give optimal subsequences that end on later elements, and if an increasing subsequence ends on a small value, then it is useful because it is versatile concerning what may be appended to the end, but if it is short and it ends on a large value, then it is not very useful. In the 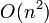 algorithm already described, a lot of time is spent looking at possibly useless increasing subsequences; for example, when computing
algorithm already described, a lot of time is spent looking at possibly useless increasing subsequences; for example, when computing 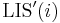 , we examine all values of
, we examine all values of 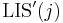 , where
, where 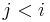 , even though some
, even though some 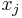 's may be larger than
's may be larger than  .
.
Thus we will maintain an auxiliary array  indexed by LIS length. The entry
indexed by LIS length. The entry ![a[i]](/wiki/images/math/5/9/5/595711c58954cfc2eb727cba561e3512.png) will, at any given time, hold the least possible value for the last element of an increasing subsequence of
will, at any given time, hold the least possible value for the last element of an increasing subsequence of  of length
of length  composed of elements we have so far examined. Initially all entries of
composed of elements we have so far examined. Initially all entries of  will be set to
will be set to 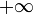 . At the conclusion of the algorithm, the highest index at which a finite value is found is the length of the LIS.
. At the conclusion of the algorithm, the highest index at which a finite value is found is the length of the LIS.
The first thing to note is that the entries of  are (non-strictly) increasing. For example, consider the sequence
are (non-strictly) increasing. For example, consider the sequence ![[9,2,6,3,1,5,0,7]](/wiki/images/math/a/3/e/a3e4109270a19cac82c7e91bec7564e4.png) . At the conclusion of the algorithm, the array
. At the conclusion of the algorithm, the array  will contain the values
will contain the values ![[0,3,5,7,+\infty,+\infty,+\infty,+\infty]](/wiki/images/math/e/d/f/edf8093f85a066c41d1b2a9844332692.png) . This tells us that the last element of any increasing subsequence of length 1 will be at least 0, the last element of any increasing subsequence of length 2 will be at least 3, and so on; the infinite values indicate that subsequences of those lengths do not exist. We know that
. This tells us that the last element of any increasing subsequence of length 1 will be at least 0, the last element of any increasing subsequence of length 2 will be at least 3, and so on; the infinite values indicate that subsequences of those lengths do not exist. We know that  is increasing because it would be absurd if it were not. For example, suppose that
is increasing because it would be absurd if it were not. For example, suppose that 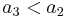 , so that the least last element attainable for an increasing sequence of length 3 were less than the least last element attainable for an increasing sequence of length 2. Then we could remove the last element from the sequence of length 3 to obtain an even smaller element (possibly) at the end of an increasing sequence of length 2, which contradicts the optimality of the value we already have on file.
, so that the least last element attainable for an increasing sequence of length 3 were less than the least last element attainable for an increasing sequence of length 2. Then we could remove the last element from the sequence of length 3 to obtain an even smaller element (possibly) at the end of an increasing sequence of length 2, which contradicts the optimality of the value we already have on file.
Now let's see how the array  allows us to find the length of the LIS. We consider the elements of
allows us to find the length of the LIS. We consider the elements of  one at a time starting from
one at a time starting from 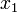 . For each element
. For each element  we consider, we notice that we want to find the longest increasing subsequence so far discovered that ends on a value less than or equal to
we consider, we notice that we want to find the longest increasing subsequence so far discovered that ends on a value less than or equal to  . To do this, we perform a binary search on the array
. To do this, we perform a binary search on the array  for the largest index
for the largest index  for which
for which 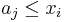 , or return
, or return 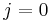 if no such index exists (empty sequence). Then, we know we can obtain an increasing subsequence of length
if no such index exists (empty sequence). Then, we know we can obtain an increasing subsequence of length 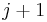 by appending
by appending  to the end of the increasing subsequence of length
to the end of the increasing subsequence of length  ending at on value
ending at on value 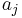 ; if there is no such value then we get an increasing subsequence of length 1 by taking
; if there is no such value then we get an increasing subsequence of length 1 by taking  by itself. What effect does this have on
by itself. What effect does this have on  ? We know that
? We know that 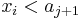 , and we also know that we have obtained an increasing subsequence of length
, and we also know that we have obtained an increasing subsequence of length 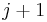 whose last element is
whose last element is  , which is therefore better than what we have on file for
, which is therefore better than what we have on file for 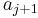 . Therefore, we update
. Therefore, we update 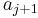 so that it equals
so that it equals  . Note that after this operation,
. Note that after this operation,  will still be sorted, because
will still be sorted, because  was originally less than
was originally less than 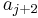 , so
, so 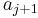 will be less after the update, and
will be less after the update, and 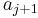 will still be greater than or equal to
will still be greater than or equal to 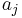 , because
, because 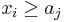 . After iterating through all elements of
. After iterating through all elements of  and updating
and updating  at each step, the algorithm terminates.
at each step, the algorithm terminates.
Pseudocode
(Non-strict case.)
input x
n ← length of x
result ← 0
a[0] ← -∞
for each i ∈ [1..n]
a[i] ← +∞
for each i ∈ [1..n]
l ← 0
u ← n
while u > l
if a[⌊(l+u)/2⌋] ≤ x[i]
l ← 1 + ⌊(l+u)/2⌋
else
u ← ⌊(l+u)/2⌋
a[l] ← x[i]
result ← max(result,l)
return result
Analysis
The reason why we expect this algorithm to be more efficient is that, by examining only  instead of the preceding
instead of the preceding  -values, all the irrelevant increasing subsequences (the ones that are both short and high at the end) are ignored, as they cannot "win" on either front and hence secure a position in
-values, all the irrelevant increasing subsequences (the ones that are both short and high at the end) are ignored, as they cannot "win" on either front and hence secure a position in  .
.
Time
The time taken for a binary search in the auxiliary array, of size  , is
, is 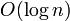 , and one is executed as each element of
, and one is executed as each element of  is examined. Therefore this algorithm achieves the stated time bound of
is examined. Therefore this algorithm achieves the stated time bound of 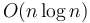 .
.
Memory
Still 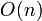 , as our auxiliary array has size
, as our auxiliary array has size  .
.
References
- ↑ Fredman, Michael L. (1975), "On computing the length of longest increasing subsequences", Discrete Mathematics 11 (1): 29–35, doi:10.1016/0012-365X(75)90103-X
![\operatorname{LIS}'(i) = (\text{the longest out of } (\{\operatorname{LIS}'(j) \mid 1 \leq j < i \wedge x_j \leq x_i\} \cup \{[\,]\}))x_i](/wiki/images/math/e/5/5/e55474191f01c6dcdf11484eb608b408.png)