Difference between revisions of "Segment tree"
(Created page with 'The '''segment tree''' is a highly versatile data structure, based upon the divide-and-conquer paradigm, which can be thought of as a tree of intervals of …') |
|||
| Line 3: | Line 3: | ||
==The problem== | ==The problem== | ||
Before introducing the structure of the segment tree, we will consider the motivation for its existence. Suppose that you are initially given an array of numbers (natural, integral, real, it doesn't matter) and a series of operations to be performed one after another. Each operation will ask you either to find the sum of all elements within a specified range of indices or to modify one of the array's elements to a new, specified value. For example, suppose the initial array is [9,2,6,3,1,5,0,7] and you are asked to find the sum of the 3rd through 6th elements, inclusive. Then you would answer 15 (which is 6+3+1+5). Next, you are asked to change the 5th element to 8. Then, you are asked for the sum of the 4th through 8th elements. You answer 23 (which is 3+8+5+0+7). | Before introducing the structure of the segment tree, we will consider the motivation for its existence. Suppose that you are initially given an array of numbers (natural, integral, real, it doesn't matter) and a series of operations to be performed one after another. Each operation will ask you either to find the sum of all elements within a specified range of indices or to modify one of the array's elements to a new, specified value. For example, suppose the initial array is [9,2,6,3,1,5,0,7] and you are asked to find the sum of the 3rd through 6th elements, inclusive. Then you would answer 15 (which is 6+3+1+5). Next, you are asked to change the 5th element to 8. Then, you are asked for the sum of the 4th through 8th elements. You answer 23 (which is 3+8+5+0+7). | ||
| + | |||
===Naive algorithm=== | ===Naive algorithm=== | ||
| + | One could merely store the array of numbers as a simple array, updating in <math>\mathcal{O}(1)</math> time whenever necessary and querying by looping over the range specified, adding the elements contained within. This latter step, however, can take <math>\mathcal{O}(N)</math> time when the size of the range is <math>\mathcal{O}(N)</math>. It is also possible to store the [[prefix sum]]s of the array, so that queries can be performed in <math>\mathcal{O}(1)</math> time but updates can take <math>\mathcal{O}(1)</math> when the element to be updated is near the end of the array. Thus, if the number of queries is low compared to the number of queries, the former solution might be practical; similarly, if there are many more queries than updates, the latter might be practical. However, what if there are an approximately equal number of queries and updates? | ||
| + | |||
| + | === | ||
Revision as of 00:22, 27 December 2009
The segment tree is a highly versatile data structure, based upon the divide-and-conquer paradigm, which can be thought of as a tree of intervals of an underlying array, constructed so that queries on ranges of the array as well as modifications to the array's elements may be efficiently performed.
The problem
Before introducing the structure of the segment tree, we will consider the motivation for its existence. Suppose that you are initially given an array of numbers (natural, integral, real, it doesn't matter) and a series of operations to be performed one after another. Each operation will ask you either to find the sum of all elements within a specified range of indices or to modify one of the array's elements to a new, specified value. For example, suppose the initial array is [9,2,6,3,1,5,0,7] and you are asked to find the sum of the 3rd through 6th elements, inclusive. Then you would answer 15 (which is 6+3+1+5). Next, you are asked to change the 5th element to 8. Then, you are asked for the sum of the 4th through 8th elements. You answer 23 (which is 3+8+5+0+7).
Naive algorithm
One could merely store the array of numbers as a simple array, updating in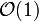 
time whenever necessary and querying by looping over the range specified, adding the elements contained within. This latter step, however, can take 
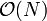time when the size of the range is 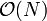. It is also possible to store the prefix sums of the array, so that queries can be performed in 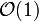time but updates can take 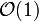when the element to be updated is near the end of the array. Thus, if the number of queries is low compared to the number of queries, the former solution might be practical; similarly, if there are many more queries than updates, the latter might be practical. However, what if there are an approximately equal number of queries and updates?
