Difference between revisions of "Depth-first search"
(→Recursive implementation) |
|||
| Line 1: | Line 1: | ||
| + | [[File:DFS.gif|thumb|right|250px|Animated example of DFS.]] | ||
| + | |||
'''Depth-first search''' (DFS) is one of the most-basic and well-known types of algorithm in [[graph theory]]. The basic idea of DFS is deceptively simple, but it can be extended to yield asymptotically optimal solutions to many important problems in graph theory. It is a type of [[graph search]] (what it means to ''search'' a graph is explained in that article). | '''Depth-first search''' (DFS) is one of the most-basic and well-known types of algorithm in [[graph theory]]. The basic idea of DFS is deceptively simple, but it can be extended to yield asymptotically optimal solutions to many important problems in graph theory. It is a type of [[graph search]] (what it means to ''search'' a graph is explained in that article). | ||
Revision as of 03:26, 17 November 2009
Depth-first search (DFS) is one of the most-basic and well-known types of algorithm in graph theory. The basic idea of DFS is deceptively simple, but it can be extended to yield asymptotically optimal solutions to many important problems in graph theory. It is a type of graph search (what it means to search a graph is explained in that article).
Contents
Principles of DFS
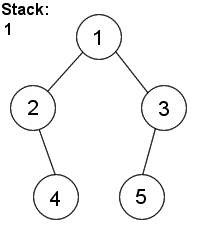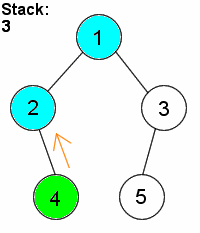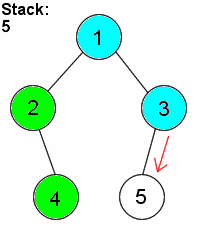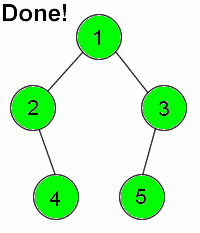
DFS is distinguished from other graph search techniques in that, after visiting a vertex and adding its neighbours to the fringe, the next vertex to be visited is always the newest vertex on the fringe, so that as long as the visited vertex has unvisited neighbours, each neighbour is itself visited immediately. For example, suppose a graph consists of the vertices {1,2,3,4,5} and the edges {(1,2),(1,3),(2,4),(3,5)}. If we start by visiting 1, then we add vertices 2 and 3 to the fringe. Suppose that we visit 2 next. (2 and 3 could have been added in any order, so it doesn't really matter.) Then, 4 is placed on the fringe, which now consists of 3 and 4. Since 4 was necessarily added after 3, we visit 4 next. Finding that it has no neighbours, we visit 3, and finally 5.
Stack-based implementation of DFS
The basic template given at Graph search can be easily adapted for DFS:
input G
for all u ∈ V(G)
let visited[u] = false
for each u ∈ V(G)
if visited[u] = false
let S be empty
push(S,u)
while not empty(S)
v = pop(S)
if visited[v] = false
visit v
visited[v] = true
for each w ∈ V(G) such that (v,w) ∈ E(G) and visited[w] = false
push(S,w)
F has been replaced by a stack, S, because a stack satisfies exactly the necessary property for DFS: the most recently added item is the first to be removed.
Recursive implementation of DFS
There is a much cleaner implementation of DFS using recursion. Notice that no matter which vertex we happen to be examining, we execute the same code. That suggests that we might be able to wrap this code in a recursive function, in which the argument is the vertex to be visited next. Also, after a particular vertex is visited, we know that we want to immediately visit any of its unvisited neighbours. We can do so by recursing on that vertex:
function DFS(u)
if not visited[u]
visit u
visited[u] = true
for each v ∈ V(G) such that (u,v) ∈ E(G)
DFS(v)
input G
for each u ∈ V(G)
let visited[u]=false
for each u ∈ V(G)
DFS(u)
Note that we do not need to check if a vertex has been visited before recursing on it, because it is checked immediately after recursing.
Performance characteristics of DFS
Time
Most DFS algorithms feature a constant time "visit" operation. Suppose, for the sake of simplicity, that the entire graph consists of one connected component. Each vertex will be visited exactly once, with each visit being a constant-time operation, so 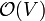 time is spent visiting vertices. Whenever a vertex is visited, every edge radiating from that vertex is considered, with constant time spent on each edge. It follows that every edge in the graph will be considered exactly twice -- once for each vertex upon which it is incident. Thus, the time spent considering edges is again a constant factor times the number of edges,
time is spent visiting vertices. Whenever a vertex is visited, every edge radiating from that vertex is considered, with constant time spent on each edge. It follows that every edge in the graph will be considered exactly twice -- once for each vertex upon which it is incident. Thus, the time spent considering edges is again a constant factor times the number of edges, 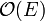 . This makes DFS
. This makes DFS 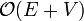 overall, linear time, which, like BFS, is asymptotically optimal for a graph search.
overall, linear time, which, like BFS, is asymptotically optimal for a graph search.
Space
Recursive implementation
For every additional level of recursive depth, a constant amount of memory is required. Notice that on the recursive stack, no vertex may be repeated (except the one at the top, in the current instance, just before the if not visited[u] check), because a vertex must be marked visited before any vertices can be pushed onto the stack above it, and recursion stops when a vertex is encountered which has already been marked visited. Therefore, DFS requires 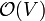 additional memory, and can be called "linear space". In practice this is often less than the memory used to store the graph in the first place, if the graph is explicit (
additional memory, and can be called "linear space". In practice this is often less than the memory used to store the graph in the first place, if the graph is explicit (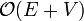 space with an adjacency list).
space with an adjacency list).
Non-recursive implementation
The less-preferred non-recursive implementation cannot be guaranteed to take only 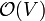 additional memory, since vertices are not visited immediately after being pushed on the stack (and therefore a vertex may be on the stack several times at any given moment). However, it is also clear that there can be no more than
additional memory, since vertices are not visited immediately after being pushed on the stack (and therefore a vertex may be on the stack several times at any given moment). However, it is also clear that there can be no more than 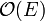 vertices on the stack at any given time, because every addition of a vertex to the stack is due to the traversal of an edge (except for that of the initial vertex) and no edge can be traversed more than twice. The stack space is therefore bounded by
vertices on the stack at any given time, because every addition of a vertex to the stack is due to the traversal of an edge (except for that of the initial vertex) and no edge can be traversed more than twice. The stack space is therefore bounded by 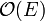 , and it is easy to see that a complete graph does indeed meet this upper bound.
, and it is easy to see that a complete graph does indeed meet this upper bound. 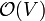 space is also required to store the list of visited vertices, so
space is also required to store the list of visited vertices, so 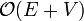 space is required overall.
space is required overall.
Applications of DFS
DFS, by virtue of being a subcategory of graph search, is able to find connected components, paths (including augmenting paths), spanning trees, and topological orderings in linear time. The special properties of DFS also make it uniquely suitable for finding biconnected components (or bridges and articulation points) and strongly connected components. There are three well-known algorithms for the latter, those of Tarjan, Kosaraju, and Gabow.
The following example shows how to find connected components and a spanning forest (a collection of spanning trees, one for each connected component) with DFS.
function DFS(u,v)
if id[v] = -1
id[v] = cnt
let pred[v] = u
for each w ∈ V(G) such that (v,w) ∈ E(G)
DFS(v,w)
input G
cnt = 0
for each u ∈ V(G)
let id[u] = -1
for each u ∈ V(G)
if id[u] = -1
DFS(u,u)
cnt = cnt + 1
After the termination of this algorithm, cnt will contain the total number of connected components, id[u] will contain an ID number indicating the connected component to which vertex u belongs (an integer in the range [0,cnt)) and pred[u] will contain the parent vertex of u in some spanning tree of the connected component to which u belongs, unless u is the first vertex visited in its component, in which case pred[u] will be u itself.