Secret Room
Hmm, now why would someone break into a mundane software company?After looking at the building blueprints (to place cameras), you've noticed the suspicious room at the top.
Investigating a little, you find no visible entrance - but there's a strange humming noise emanating from the room.
Upon asking your manager you are ushered into the conference room where a confidential meeting seems to be taking place.
It seems that this secret room holds a certain treasure: the thishasbeencensored
Now, they want to secure this room with lethal green laser beams.
The lasers are very thin, but they have the ability to burn a hole through an intruder instantly.
The company engineers have built several laser designs, and they'd like to choose the best one.
To make a laser design effective, they want to minimize the freedom a thief would have while in the room.
As an estimate, they'd like to find the largest circle that could fit anywhere without hitting a laser.
Now, doing this by hand would be quite tedious - so write a program to do it for them!
Input
Two positive integers, W and H (W,H ≤ 10,000) representing the width and height of the room.Then, an integer N ≤ 50, representing the number of laser beams.
For each laser beam:
4 integers, (x1,y1),(x2,y2) representing one laser beam.
A laser beam will travel between those two points (they are guaranteed to be on the wall).
The room will be modeled as a 2-D grid - (0,0) being the lower left and (W,H) the upper right.
Output
The radius of the largest circle that could fit without being cut by lasers.Your answer should be correct to 4 decimal places.
Sample Input
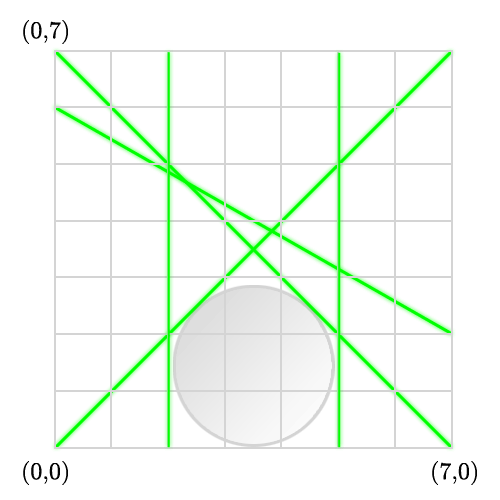
7 7 5 0 0 7 7 0 7 7 0 0 6 7 2 2 0 2 7 5 0 5 7
Sample Output
1.4497
The exact answer is 3.5(√2 - 1) = 1.449747...
(Try calculating it! Please don't try coordinate geometry :P)
Diagram
All Submissions
Best Solutions
Point Value: 25 (partial)
Time Limit: 2.00s
Memory Limit: 16M
Added: Feb 15, 2009
Author: hansonw1
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)
If it helps, you can use this python program to draw test cases. (I used this to check my test data) (It is pretty picky with how you input your data - use the same format as the sample input) [code]import Tkinter, os from Tkinter import * W, H = map(int, raw_input("Width and height? (W H) ").split(" ")) wscale = 1. * W / max(W, H) * 800 hscale = 1. * H / max(W, H) * 800 def pt(x, y): x = 5 + 1. * x / W * wscale y = 5 + hscale - 1. * y / H * hscale return x,y root = Tk() canvas = Canvas(root, width=wscale+10, height=hscale+10) canvas.pack() canvas.create_line(pt(0,0), pt(0,H)) canvas.create_line(pt(0,H), pt(W,H)) canvas.create_line(pt(W,H), pt(W,0)) canvas.create_line(pt(W,0), pt(0,0)) N = int(raw_input("Number of lines? (N) ")) for i in range(N): x1,y1,x2,y2 = map(int, raw_input("Line: (x1 y1 x2 y2) ").split(" ")) canvas.create_line(pt(x1,y1), pt(x2,y2), fill="red") #If you want, you can draw a circle to see if it lines up sz = float(raw_input("Radius of the circle? (R) ")) x, y = map(float, raw_input("Centre of the circle (x y)? ").split(" ")) canvas.create_oval(pt(x-sz,y-sz), pt(x+sz,y+sz)) root.mainloop()[/code](It is pretty picky with how you input your data - use the same format as the sample input)