IOI '00 - Beijing, China
Building with Blocks
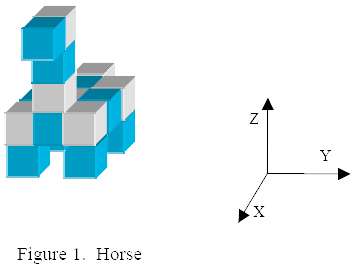
A unit cube is a 1x1x1 cube, whose corners have integer x, y, and z coordinates. Two unit cubes are connected when they share a face. A 3-dimensional solid object (solid, for short) is a non-empty connected set of unit cubes (see Figure 1). The volume of a solid is the number of unit cubes it contains. A block is a solid with volume at most 4. Two blocks have the same type when one can be obtained from the other by translations and rotations (not reflections). There are exactly 12 block types (see Figure 2). The colors in the figures only help to clarify the structure of the solids; they have no other meaning.
A set D of blocks is a decomposition of a solid S when the union of all blocks in D equals S, and no two distinct blocks in D have a unit cube in common.
Your task is to write a program that, given a description of the block types and a solid S, determines a smallest set of blocks into which S can be decomposed. It only needs to report the types of these blocks as often as they occur in the decomposition.
Input
In the input, we identify a unit cube by a line with three integers x, y, and z, being the coordinate triple of its corner that minimizes x + y + z. The input is divided into two parts, which were originally in two separate files but have been combined out of necessity for this online judge.
The first part of input describes the 12 block types and will be the same for all evaluation runs. It contains the descriptions of the 12 block types in Figure 2, sorted on type number. Each block type is described by a group of consecutive lines. The first line contains the integer I identifying the block type (1 ≤ I ≤ 12). The second line contains the volume V of the block type (1 ≤ V ≤ 4). The remaining V lines contain three integers x, y and z, each being one unit cube of the block type (1 ≤ x, y, z ≤ 4).
The second part of input describes the solid. The first line contains the volume V of the solid (1 ≤ V ≤ 50). The remaining V lines contain three integers x, y, z, each being one unit cube of the solid (1 ≤ x, y, z ≤ 7).
Output
The first line must contain one integer M, being the smallest number of blocks into which the input solid can be decomposed. The second line lists M type identifiers of the block types into which the input solid can be decomposed. There may be several solutions for each input file, and your program needs to output only one of them. The order of the numbers in the second line is immaterial.Sample Input
1 1 1 1 1 2 2 1 1 1 1 2 1 3 3 1 1 1 1 2 1 1 3 1 4 3 1 1 1 1 2 1 1 1 2 5 4 1 1 1 1 2 1 1 3 1 1 4 1 6 4 1 1 1 1 2 1 1 1 2 1 2 2 7 4 1 1 1 1 2 1 1 1 2 1 1 3 8 4 1 1 1 1 2 1 1 3 1 1 2 2 9 4 1 2 1 1 3 1 1 1 2 1 2 2 10 4 2 1 1 1 2 1 2 2 1 2 1 2 11 4 1 1 1 1 2 1 2 2 1 1 1 2 12 4 2 2 1 2 1 2 1 2 2 2 2 2 18 2 1 1 4 1 1 2 3 1 4 3 1 2 1 2 3 1 2 4 1 2 1 2 2 2 2 2 3 2 2 4 2 2 2 3 2 3 3 2 4 3 2 4 2 3 4 2 4 4 2 5 5 2 5
Sample Output
5 7 10 2 10 12
The solid described in the sample input is the "horse" of Figure 1.
Note that the following, as well as all of their respective permutations, are also possibilities for the second line of output:
2 7 10 11 12 2 7 11 11 12 4 4 7 10 11 4 4 9 10 11
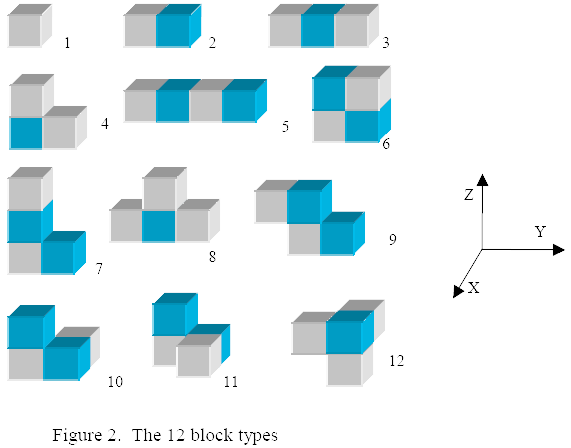
All Submissions
Best Solutions
Point Value: 20 (partial)
Time Limit: 2.00s
Memory Limit: 16M
Added: Aug 23, 2009
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)
It's quiet in here...